Question 676108: How is adding radical expressions different to adding polynomial expressions?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! To add polynomials you only have to add like terms, radicals might not even add.
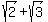 can't be the square root of anything, because if you square it, you still get a radical expression: can't be the square root of anything, because if you square it, you still get a radical expression:
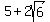 so you can't simplify it at all so you can't simplify it at all
Sometimes, radical expressions may be written as exponential expressions by changing them into a fraction:
for example, the  can also be written as can also be written as 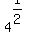 , while the cube root of , while the cube root of  is is 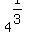 , and so on. But they are still distinguished because the exponents are in fractional form. , and so on. But they are still distinguished because the exponents are in fractional form.
Adding radical expressions is more general because the radicals could be in the denominator as well. Or, you might have to simplify something in order to add them.
When you are adding polynomial expressions, you can only add like terms (or terms of the same degree).
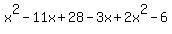
 and and  are like terms so you can add them to get are like terms so you can add them to get 
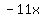 and and 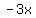 are like terms so you can add them to get are like terms so you can add them to get 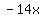
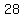 and and  are like terms so you can add them to get are like terms so you can add them to get 
When you add radical expressions, the number under the radical (the radicand), is like an . You can only add these if the radicand are the same. . You can only add these if the radicand are the same.


but

|
|
|