SOLUTION: A football initially on the found is kicked in the air and follows a parabolic path after 2 seconds the football is 6 meters off the ground, it reaches its maximum height of 8 met

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: A football initially on the found is kicked in the air and follows a parabolic path after 2 seconds the football is 6 meters off the ground, it reaches its maximum height of 8 met      Log On


   

Question 675504: A football initially on the found is kicked in the air and follows a parabolic path after 2 seconds the football is 6 meters off the ground, it reaches its maximum height of 8 meters after 4 seconds. Find the height of the football 7 seconds after the ball is kicked?
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
The standard quadratic equation is:
y+=+ax%5E2%2Bbx%2Bc
In this problem, x will represent the time and y will represent the height.

The "c" in this equation is the y-intercept. Since the ball starts (x=0) on the ground (y = 0), c is 0. So our equation will have the form:
y+=+ax%5E2%2Bbx
Now all we have to do is figure out the values for "a" and "b".

The problem tells us that at 2 seconds the ball is 6 feet in the air. So the point (2, 6) is on this parabola and must fit our equation:
6+=+a%2A%282%29%5E2+%2B+b%2A2
We are also told that after 4 seconds the ball is 8 feet in the air. So the point (4, 8) must also be on the parabola and fit our equation:
8+=+a%2A%284%29%5E2+%2B+b%2A4
With these two equations we should be able to solve for a and b.

However, there is a slightly faster way to find a and b. We are told that the height of 8 is the maximum height. This means that (4, 8) is not just any point on the parabola. It is the vertex of the (downward-opening) parabola. This fact can be exploited to find a and b a little faster than solving the two-equation system above. One way to take advantage of knowing the vertex uses the fact that the x-coordinate of the vertex of a parabola is always -b/2a. So
equation to find a and b. This system is easier and faster to solve since one equation, -8a = b, is already solved for b. Substituting for b in the other equation we get:
6+=+a%2A%282%29%5E2+%2B+%28-8a%29%2A2
Simplifying...
6+=+a%2A4+%2B+%28-8a%29%2A2
6+=+4a+%2B+%28-16a%29
6+=+-12a
Dividing by -12:
-1%2F2+=+a
Now we can find b:
b+=+-8a
b+=+-8%28-1%2F2%29
b+=+4
With a = -1/2 and b = 4 our equation is:
y+=+%28-1%2F2%29x%5E2%2B4x

Now we can use this to find the height at 7 seconds:
y+=+%28-1%2F2%29%287%29%5E2%2B4%287%29
y+=+%28-1%2F2%2949%2B4%287%29
y+=+-49%2F2%2B28
y+=+-49%2F2%2B56%2F2
y+=+9%2F2+=+4%261%2F2
So the ball will be 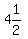4%261%2F2 feet off the ground after 7 seconds.

Notes:
  • You get the same values for a and b if you solve the original system of:
    6+=+a%2A%282%29%5E2+%2B+b%2A2
    and
    8+=+a%2A%284%29%5E2+%2B+b%2A4
  • If you don't know (or can't remember) that the x-coordinate of the vertex is -b/2a there is another way to take advantage of the vertex. Parabolas are symmetric about the vertical line through the vertex. Since it took 4 seconds to get from the ground to the highest point it will take another 4 seconds to come back to the ground. So (8, 0) will be another point on this parabola. With the two x-intercepts of 0 (from (0, 0)) and 8 (from (8, 0)) we can write the equation of the parabola in a different way:
    y+=+k%2A%28x-0%29%28x-8%29
    Simplifying...
    y+=+k%2Ax%2A%28x-8%29
    y+=+k%2Ax%5E2-8kx
    And we can use with (2, 6) or (4, 8) to find k:
    6+=+k%2A%282%29%5E2-8k%282%29%29
    6+=+k%2A4-8k%282%29
    6+=+k%2A4-16k
    6+=+-12k
    -1%2F2+=+k
    Substituting this back into:
    y+=+k%2Ax%5E2-8kx
    y+=+%28-1%2F2%29%2Ax%5E2-8%28-1%2F2%29x
    y+=+%28-1%2F2%29%2Ax%5E2%2B4x