SOLUTION: What is the number of square units in the area of a triangle whose sides are 5, 6 and &#8730;<span style="text-decoration: overline">61</span>. Explain answers in simplest form.

Algebra ->  Triangles -> SOLUTION: What is the number of square units in the area of a triangle whose sides are 5, 6 and &#8730;<span style="text-decoration: overline">61</span>. Explain answers in simplest form.       Log On


   

Question 674652: What is the number of square units in the area of a triangle whose sides are 5, 6 and √61. Explain answers in simplest form. (I think it's 21, but i think it's wrong.)
Found 2 solutions by Edwin McCravy, MathTherapy:
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
What is the number of square units in the area of a triangle whose sides are 5, 6 and √61. Explain answers in simplest form. (I think it's 21, but i think it's wrong.) 

This is a right triangle because it satisfies the Pythagorean theorem

a = 5, b = 6 and c = √61

a˛ + b˛ = c˛
5˛ + 6˛ = (√61)˛
25 + 36 = 61
     61 = 61

Therefore it looks like this:



Therefore its base b = 5 and its height h = 6.  The formula
for the area of a triangle is  

             A = 1%2F2bh
             A = 1%2F2(5)(6)
             A = 1%2F2(30)
             A = 15 square units.

The way to check it is to draw a 5×6 rectangle:



Realize that the triangle above is one-half of its area 
because if you draw the diagonal it cuts the 5×6 rectangle 
into two right triangles just exactly like the one above.



and if you tile it off into square units like this:



You can see that there are 30 square units and since the
triangle has half as many square units of area as the rectangle,
then the triangle must have half of 30 square units of area or 15
square units of area.

Edwin

Answer by MathTherapy(10551) About Me  (Show Source):
You can put this solution on YOUR website!
What is the number of square units in the area of a triangle whose sides are 5, 6 and √61. Explain answers in simplest form. (I think it's 21, but i think it's wrong.)

You never bothered to share with us how you arrived at 21 sq units.

However, you need to use the law of cosines formula, a%5E2+=+b%5E2+%2B+c%5E2+-+2bc+Cos+A
After substituting the sides (based on their angles), into the above-formula, you will derive the degree measure of angle A.

Using the degree measure of angle A, you can then determine the area of the triangle by applying the following formula for a non-right triangle: A+=+%281%2F2%29bc+Sin+A

This should give you an area of 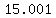15.001 ≈ highlight_green%2815%29 sq units

OR

It can be seen that the triangle is actually a right-angled one, so you can use the pythagorean formula: a%5E2+%2B+b%5E2+=+c%5E2, with c being the longest side, or the hypotenuse of the triangle, represented by sqrt%2861%29.

Send comments and “thank-yous” to “D” at MathMadEzy@aol.com