|
Question 674302: Can someone walk me through the steps for the following problem? Thank you!
144-25t+t^2
1. Factor completely.
2. Remember to look first for a common factor.
3. Check by multiplying.
4. If a polynomial is prime, state this.
Found 2 solutions by Theo, solver91311:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! this time around i'll take you through this the way i would look at it.
the equation is 144 - 25t + t^2
first thing i would do is re-order the terms so the highest level term is on the left and the lowest level term is on the right.
the equation becomes t^2 + 25t - 144
next thing i would do is notice that the coefficient of the t^2 term is equal to 1.
this is good because it makes trying to find the factors of this equation easier.
next thing i would do is determine what factors i need to multiply together to get -144.
all of the possible combinations i could find are:
-1 * 144 = -144
-2 * 72 = -144
-3 * 48 = -144
-4 * 36 = -144
-6 * 24 = -144
-8 * 18 = -144
-9 * 16 = -144
-12 * 12 = -144
-16 * 9 = -144
-18 * 8 = -144
-24 * 6 = -144
-36 * 4 = -144
-48 * 3 = -144
-72 * 2 = -144
-144 * 1 = -144
these are all of the possible combinationss of factors that, when you multiply them together, you get -144.
now i have to find which of these can be added together to get +25.
here goes:
-1 + 144 = 143
-2 + 72 = 70
-3 + 48 = 45
-4 + 36 = 32
-6 + 24 = 18
-8 + 18 = 10
-9 + 16 = 7
-12 + 12 = 0
-16 + 9 = -7
-18 + 8 = -10
-24 + 6 = -18
-36 + 4 = -32
-48 + 3 = -45
-72 + 2 = -70
-144 + 1 = -143
none of these add up to +25.
therefore, there are no factors that are integers and the polynomial is prime.
as i told you before, you can graph the equation to see if it has any roots and where those roots are and how many you have (you can have 2 or 1 or none).
you can always solve a quadratic equation using the quadratic formula. it will also tell you if the roots are integers and if they are real and how many of them you have (you can have 2 or 1 or none)
this is the process that is followed when you are looking for factors to the equation.
here's an example where the process is used and the factors can be found.
suppose the equation is x^2 + 5x + 4.
you want to find the roots.
take the constant term and determine what factors can be multiplied together to equal it.
those factors are:
4 * 1 = 4
2 * 2 = 4
1 * 4 = 4
-4 * -1 = 4
-2 * -2 = 4
-1 * -4 = 4
now look for which of these factors will add up to equal the coefficient of the x term.
you get:
4 + 1 = 5 *****
2 + 2 = 4
1 + 4 = 5 *****
-4 + -1 = -5
-2 + -2 = -4
-1 + -4 = -5
you can see that 4 + 1 or 1 + 4 will add up to 5 (the coefficient of the middle term) and that 4 * 1 or 1 * 4 will multiply together to equal 4 (the constant term)
those are your potential factors.
your equation is x^2 + 5x + 4
try (x + 4) * (x + 1)
when you multiply these factors together you get:
x^2 + x + 4x + 4 which simplifies to x^2 + 5x + 4
bingo !!!!!
you found the factors.
they are (x + 4) and (x + 1)
now you want to find the roots.
you set (x + 4) * (x + 1) = 0
you set each of the factors equal to 0
you get:
x + 4 = 0 and x + 1 = 0
you solve for x in each equation and you get:
x = -4 and x = -1
those are the roots of your equation.
the same method was used only this time you were able to find the factors.
you can graph both equation we worked on.
the first equation is t^2 + 25t - 144
in order to graph it, you have to replace t with x to make the equation:
x^2 + 25x - 144.
now you can use the graphing software to graph it.
the graph will look like this:
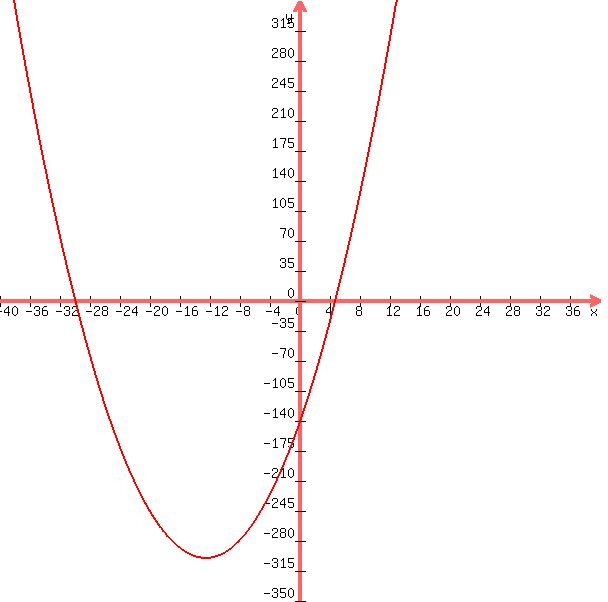
you can see from the graph that the roots do not appear to be integers which was confirmed by the fact that you couldn't find the factors.
the second equation is x^2 + 5x + 4
the graph will look like this:
this graph looks more like the roots are integers which means you should be able to factor it which we confirmed by finding the factors.
if in doubt, use the quadratic formula.
that will find you the roots, tell you whether you have roots, tell you whether those roots are integers or now and tell you how many roots you have (0, 1, or 2).
if the quadratic formula gives you integers as roots, then you can factor the equation.
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website!
Ok, Scruffy, go get your leash and collar and we'll take a walk.
Put your trinomial in standard form:
We are looking for two factors of the form  and  such that  ,  , and  . We get to use coefficients of 1 on the  terms because the lead coefficient in the given trinomial is 1.
In order for the sum to be negative and the product to be positive, both of the  and  values must be negative.
So what are the possible integer factors of 144?
-1 -144 : -1 X -144 = 144, but -1 + -144 = -145 ≠ -25
-2 -72 : -2 X -72 = 144, but -2 + -72 = -74 ≠ -25
-3 -48 :
-4 -36 :
-6 -24 :
-8 -18 :
-9 -16 :
-12 -12 :
You fill in the rest of the table above and determine whether an appropriate pair of integers exists. If it does, that is your solution, if not, the polynomial is prime.
John
My calculator said it, I believe it, that settles it
|
|
|
| |
