Question 674243: Bob spent 1/6 of his life as a child, 1/12 as an adolescent, and 1/7 as a bachelor, five years after he was married, he had a son who died 4 years before his father at half his father's final age. How long did bob live?
Found 3 solutions by Theo, ikleyn, greenestamps:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! he spent 1/6 of his life as a child, 1/12 as an adolescent, and 1/7 as a bachelor.
5 years after he's married, he has a son.
son dies 4 years before his father at half his father's final age.
how long did he live?
if we add up 1/6 and 1/12 and 1/7, we get 33/84.
this should mean that he dies at 84 and has 51 years left to live.
if that holds up, then we found the answer.
let's see if it does.
assuming we're right, then he gets married at 33 years of age.
5 years later he has a son when he is 38 years old.
based on our assumption, he dies at 84.
his son has died 4 years earlier at half his age when he dies which means his son has died at age 42.
here's the timeline.
his age his son's age description of event
38 0 his son is born.
80 42 his son dies.
84 he dies.
when his son dies at 42, he is 80 (80 - 38 = 42)
4 years later he dies at 84.
numbers appear to check out so the solution is good.
it appears the only information we needed was to be able to add up 1/6 + 1/12 and 1/7 to find out how much of his life was consumed when he got married.
the remainder from the denominator is what he had left.
the denominator is how long he lived.
Answer by ikleyn(53427)  (Show Source):
You can put this solution on YOUR website! .
Bob spent 1/6 of his life as a child, 1/12 as an adolescent, and 1/7 as a bachelor,
five years after he was married, he had a son who died 4 years before his father
at half his father's final age. How long did bob live?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Wording in your post is not perfect, but don't despair. There is a classic
well known story problem about Diophantus, famous mathematician of ancient Greece.
Diophantus's youth lasts 1/6 of his life. He grew a beard after 1/12 more of his life.
After 1/7 more of his life, Diophantus married. Five years later, he had a son.
The son lived exactly half as long as his father, and Diophantus died just four years
after his son's death. What was his age when he died?
This story problem is precisely what you want to follow literally. So, I will solve it for you.
Again, it is classic of about 2200 years old.
Let x be the Diophantus' age when he died.
As we read the problem, we write this equation
x = 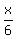 +  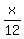+  + 5 +  + 4.
To solve, multiply all the terms by the Greatest Common Denominator, which is 12*7 = 84.
You will get
84x = 14x + 7x + 12x + 5*84 + 42x + 4*84.
Group like terms in right side
84x = (14 + 7 + 12 + 42)x + (5*84 + 4*84),
combine like terms
84x = 75x + 756,
simplify and find x
84x - 75x = 756,
9x = 756,
x = 756/9 = 84.
Thus, Diophantus died at the age of 84 years.
Solved.
About Diophantus, read this remarkable Wikipedia article
https://en.wikipedia.org/wiki/Diophantus
https://en.wikipedia.org/wiki/Diophantus
Enjoy ( ! )
Answer by greenestamps(13258)  (Show Source):
You can put this solution on YOUR website!
Solving the problem using all of the given information is a good exercise. However, logical reasoning gives the answer with very little work.
In age problems, all numbers are whole numbers. So in this problem, the age Bob lived to must be a multiple of 6, 12, and 7.
The least common multiple of 6, 12, and 7 is 84; so the age Bob lived to is an integer multiple of 84. Since twice 84 is an unreasonable answer for the age at which Bob died, the answer has to be 84.
ANSWER: 84
|
|
|
