SOLUTION: Find a quadratic equation with roots -1+4i and -1-4i

Algebra ->  Test -> SOLUTION: Find a quadratic equation with roots -1+4i and -1-4i      Log On


   

Question 674236: Find a quadratic equation with roots -1+4i and -1-4i
Found 2 solutions by ewatrrr, MathLover1:
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

The factor theorem states that a polynomial f(x) has a factor (x − k) if and only if f(k) = 0

roots -1+4i and -1-4i

f(x) = a(x-(-1+4i))(x -(-1-4i)) = a(x^2 -2x +17)

 a = 1

f(x) = x^2 -2x +17

Check product 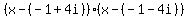%28x-%28-1%2B4i%29%29%28x+-%28-1-4i%29%29 Using FOIL

F	First terms

O	Outside terms

I	Inside terms

L	Last terms

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

a quadratic equation could be found with roots like this: Write the roots, a and b, in the form (x-a)(x-b).
%28x-a%29%28x-b%29=0
given: a=-1%2B4i and a=-1-4i..plug it in

%28x-%28-1%2B4i%29%29%28x-%28-1-4i%29%29=0

%28x%2B1-4i%29%28x%2B1%2B4i%29=0

x%5E2%2Bx%2B4i%2Ax%2Bx%2B1%2B4i-4i%2Ax-4i-16i%5E2=0



x%5E2%2Bx%2B1%2B16=0
x%5E2%2Bx%2B17=0

+graph%28+600%2C+600%2C+-10%2C+10%2C+-10%2C+20%2C+x%5E2%2Bx%2B17%29+