|
Question 673284: How do I simplify the expression and justify each step? By justify I mean each time you simplify would that step be distributive, associative, commutative etc.
29c + (-29c)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! WARNING:
Different books/teachers may give slightly different names to the same properties.
IF YOU MUST CHOOSE JUST ONE PROPERTY, AS IN A MULTIPLE CHOICE QUESTION,
then it would be simple.
I could say that 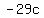 obviously means the additive inverse of obviously means the additive inverse of 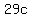 . .
Then I would say that
 is the Additive Identity Property. is the Additive Identity Property.
IF A FULL EXPLANATION IS EXPECTED,
it may be more complicated.
Unfortunately, I suspect they want to make it more complicated, and we would need to invoke 3 or more properties.
If it is interpreted as just  , we could say that , we could say that
 is the application of the Distributive Property. is the application of the Distributive Property.
Then,
 Additive Identity Property, Additive Identity Property,
and finally,
 Zero Property Zero Property
IF THEY WANT TO MAKE YOU EXPLAIN EVEN MORE:
The Distributive Property is usually represented in the form
 . .
In this case we have  , with , with  and and  . .
That is usually referred to as "taking out a common factor".
 is the same (read backwards) as is the same (read backwards) as
the usual  distributive property. distributive property.
 and and  are the same thing, are the same thing,
because of the Commutative Properties for Addition and Multiplication.
|
|
|
| |