You can
put this solution on YOUR website!
The second term in a geometric series is 36. The
sum of the first two terms is -18. What is the first
term and the common ratio?
what is the sum to infinity of the series?
Let the first term be x.
The sum of the first two terms is 18
So
x + 36 = 18
x = -18
Common ratio = 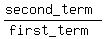 =
= 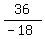 = -2
Therefore the sum to infinity is undefined because in order to
have a sum to infinity, the common ratio must be between -1 and 1,
exclusive of both.
Edwin
= -2
Therefore the sum to infinity is undefined because in order to
have a sum to infinity, the common ratio must be between -1 and 1,
exclusive of both.
Edwin