Question 672584: Here is an example of a Trig function we are working on that I HAVE been able to solve, I think:
solve trig equations algrebraically; sin^2(t)=2sin(t)+1
first set everything to zero; sin^2(t)-2sin(t)-1=0
then in this case I can use the foil method; (sin(t)-1)(sin(t)-1=0
then solve for (t); t=4.7+l(2pi) and t=pi-4.7i(2pi)
This may seem like a more simple equation but....I'm just not sure about it still. Please help me solve: sec(t) = tan(t)
I know to set everything equal to zero. sec(t)-tan(t)=0
I know sec=1/cos, but not sure if that would apply here....
thank you for your time
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is an example of a Trig function we are working on that I HAVE been able to solve, I think:
solve trig equations algrebraically; sin^2(t)=2sin(t)+1
first set everything to zero; sin^2(t)-2sin(t)-1=0
then in this case I can use the foil method; (sin(t)-1)(sin(t)-1=0
then solve for (t); t=4.7+l(2pi) and t=pi-4.7i(2pi)
---------------------------
first set everything to zero; sin^2(t)-2sin(t)-1=0
then in this case I can use the foil method; (sin(t)-1)(sin(t)-1=0
(sin(t)-1)(sin(t)-1=0
**** That doesn't factor
---------------------
Sub x for sin(t) to save typing.

| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=8 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 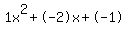 can be factored: can be factored:

Again, the answer is: 2.41421356237309, -0.414213562373095.
Here's your graph:
 |
=======================
Ignore the 1st solution, it's > 1 --> no real solution.
x = 1 - sqrt(2)
sin(t) =~ -0.41421
t = 204.47, 335.53 + n*360 degs, n = -,1,2,3...
|
|
|