|
Question 671805: Wanda paddles six miles downstream in 1 hour and her friend minnie rowing 1 mph faster goes upstream 6 miles in 2 hours. Find the speed of the current and the girls speeds/rate
I can solve it with whole numbers, but now my teacher tells me the answer should be a number rounded to the hundredths.
I tried
b-c=3mph
b+c=6mph
2b=9mph
b=4.5mph
so 4.5mph+c=6mph
c=1.33mph
but plugging that into b+c=6mph comes out to 4.5+1.33=5.83
Maybe that is close enough?
I also tried this formula from the text
Total time=distance upstream(d1)/ + (d2)distance downstream/
speed of boat upstreamm speed of boat downstream
or t= d1/r-c + d2/r+c where r=rate and c=current
but that was not working either.
Any advice on this would be tremendous.
Thanks
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Wanda paddles six miles downstream in 1 hour and her friend minnie rowing 1 mph faster goes upstream 6 miles in 2 hours. Find the speed of the current and the girls speeds/rate
I can solve it with whole numbers, but now my teacher tells me the answer should be a number rounded to the hundredths.
I tried
b-c=3mph
b+c=6mph
2b=9mph
b=4.5mph
so 4.5mph+c=6mph
c=1.33mph
but plugging that into b+c=6mph comes out to 4.5+1.33=5.83
Maybe that is close enough?
I also tried this formula from the text
Total time=distance upstream(d1)/ + (d2)distance downstream/
speed of boat upstreamm speed of boat downstream
or t= d1/r-c + d2/r+c where r=rate and c=current
but that was not working either.
Any advice on this would be tremendous.
Thanks
Let Wanda’s speed be S, and current’s speed, C
Since Wanda paddled 6 miles downstream in 1 hour, then total speed = 6 mph ( ). Adding the current's speed to hers, we can say that: S + C = 6 ------ eq (i) ). Adding the current's speed to hers, we can say that: S + C = 6 ------ eq (i)
Since Minnie paddled 6 miles upstream in 2 hours, then total speed = 3 mph (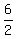 ). Subtracting the current's speed from hers, we can say that: S - C = 2 ---- eq (ii) ). Subtracting the current's speed from hers, we can say that: S - C = 2 ---- eq (ii)
S + C = 6 ----- eq (i)
S - C = 2 ----- eq (ii)
2S = 8 ---- Adding eqs (ii) & (i)
S, or Wanda’s speed = 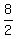 , or , or  mph mph
Minnie’s speed = S + 1, or 4 + 1, or  mph mph
4 + C = 6 ------ Substituting 4 for S in eq (i)
C, or current’s speed = 6 – 4, or  mph mph
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|
| |