Question 6717: I am horrible when it comes to word problems. I have been at this for two hours now and cannot come up with a solution. Can anyone help? It is as follows:
Using the formula of R=log(I/Io) for Richter scale:
The strongest earthquake ever to strike Japan occurred in 1933 and measure 8.9 on the Richter scale. How many times more severe was this 1933 quake than the one in May 1983 which measured 7.7 on the Richter scale?
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! First, we need to find the intensity I of the first earthquake. They said that the Richter number was 8.9.

Before we go on, there is a tricky thing about the  . It simply refers to the intensity of the faintest earthquake possible, whose value we don't have to care about, since the intensity of clearly noticeable earthquakes is written as some number times the . It simply refers to the intensity of the faintest earthquake possible, whose value we don't have to care about, since the intensity of clearly noticeable earthquakes is written as some number times the  . For practical purposes, let's just pretend that the quantity . For practical purposes, let's just pretend that the quantity 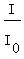 is really a single variable that simply is how many times a given earthquake is more intense than is really a single variable that simply is how many times a given earthquake is more intense than  . Let's call it simply as E for earthquake. . Let's call it simply as E for earthquake.
So,  <---- <----  Because it's the first earthquake. We now need to translate this into exponential equation. That would be: Because it's the first earthquake. We now need to translate this into exponential equation. That would be:
 <----- The base of the log becomes the base of the exponent. The exponent is the number on the other side of the equals sign from the log expression, and whatever you were logging before becomes the value that the exponent expression equals to. <----- The base of the log becomes the base of the exponent. The exponent is the number on the other side of the equals sign from the log expression, and whatever you were logging before becomes the value that the exponent expression equals to.
------------------------------------------------
Now let's find  , the intensity of the second earthquake. We start with the log equation , the intensity of the second earthquake. We start with the log equation  , which translates to the exponential equation , which translates to the exponential equation  . .
Now, we need to compare - how many more times is  more intense than more intense than  ? You simply put them on a fraction: ? You simply put them on a fraction: 
Which really is 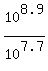 . Remember that subtraction/division rule of powers of the same base! That ratio is the same as saying . Remember that subtraction/division rule of powers of the same base! That ratio is the same as saying 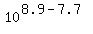 which turns out as which turns out as 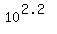 . You'd have to use a calculator to compute that. It turns out as 158.489. This means that the magnitude 8.9 earthquake is 158.489 times more intense than the 7.7 magnitude earthquake. . You'd have to use a calculator to compute that. It turns out as 158.489. This means that the magnitude 8.9 earthquake is 158.489 times more intense than the 7.7 magnitude earthquake.
|
|
|