Question 670253: For question #276198. Can someone explain the reasoning as to how this problem was solved. For example, I know that Moulders's distance = Scully's distance, that r*t = r*t. But why does 1/2 hr get added to Moulder's time? Does this mean he spends more time traveling his distance? (when you go back and plug in the answer 10 5/6 hrs into the equation, it's basically a distance equals distance equation, and this shows that Moulder takes longer to travel his distance. This is what I am basing my questions on.)
Also, how does this fit in with when Scully catches up with Moulder?
Thanks Ralph
Answer by MathTherapy(10553)   (Show Source): (Show Source):
You can put this solution on YOUR website!
For question #276198. Can someone explain the reasoning as to how this problem was solved. For example, I know that Moulders's distance = Scully's distance, that r*t = r*t. But why does 1/2 hr get added to Moulder's time? Does this mean he spends more time traveling his distance? (when you go back and plug in the answer 10 5/6 hrs into the equation, it's basically a distance equals distance equation, and this shows that Moulder takes longer to travel his distance. This is what I am basing my questions on.)
Also, how does this fit in with when Scully catches up with Moulder?
Thanks Ralph
Let the time taken by Molder to get to the “catch-up” point be T
Then time taken by Scholy to get to the “catch-up” point is T – ½hour
Molder is going to take a longer time to get to the “catch-up” point since he’s traveling at a slower speed
When Scoly catches up to Molder, both would’ve traveled the same distance
We therefore form a distance equation…one that says:
Molder’s distance traveled to “catch-up” point = Scholy’s distance traveled to the “catch-up” point, which is algebraically written as:

65T = 68T – 34
65T – 68T = - 34
– 3T = - 34
T, or time it’ll take Molder to get to “catch-up” point = 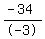 , or , or 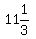 hours, or 11 hours, 20 minutes hours, or 11 hours, 20 minutes
After leaving at 8:30 AM, and after traveling for 11 hours, 20 minutes to get to “catch-up” point, Molder will reach “catch-up” point at  PM. PM.
Yes, Molder does take a longer time to cover the same distance as Scholy since he (Molder) is traveling at a slower rate of speed (65 mph as opposed to Scholy's 68 mph).
Additionally, you can either let Molder's time be T, and subtract 1/2 hour to get Scholy's time, or let Scholy's time be T, and then add 1/2 hour to get Molder's time.
Send comments and “thank-yous” to “D” at MathMadEzy@aol.com
|
|
|