Question 669841: find the center,transverse axis, vertices, foci and asymptotes of the hyperbola;
4x^2-49y^2=196
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given: 
First get it in standard form, which is either
 if the hyperbola opens right and left, if the hyperbola opens right and left,
or
 if the hyperbola opens upward and downward. if the hyperbola opens upward and downward.



note that:
the denominator of  term is greater than that of the term is greater than that of the  term, so the major axis is horizontal term, so the major axis is horizontal
Since  and and  , then , then
 and and 
so, the center is at ( , ,  ) = ( ) = ( , ,  ). ).
 and and  , ,
the equation  gives you gives you  , ,
so 
and the eccentricity is 
the vertices and foci are above and below the center, so the foci are at
( , , ) and ( ) and ( , , ), which is ), which is
( , ,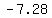 ) and ( ) and ( , , 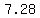 ) )
and the vertices are at ( , , ) and ( ) and ( , , ) which is ) which is
( , , ) and ( ) and ( , , ) )
Because the  part of the equation is dominant , then the slope of the part of the equation is dominant , then the slope of the
asymptotes has the a on top, so the slopes will be  . .
so, the asymptotes are  and and 
graph:


|
|
|