Question 669642: Ralph won a new fancy car worth $65,000. He plans on keeping it until he can trade it evenly for a new hybrid model that curretly costs $25,000. If the value of the fancy car decreases by 8% per year and the cost of the hybrid increases by 5% per year, then in how many years will he be able to make the trade and the values of the vehicles will be equal? Interest rate equation applies: A = Aoe^rt where: Ao = the intial value; A = value at time = t; r = rate expressed as a decimal.
Would I start two separate equations, one for depreciation and one for appreciation? Sorry, a bit lost on this one.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you needs to set the depreciation equation equal to the appreciation equation to find the point where they intersect.
if you graph the 2 equations, you will be able to see it on the graph as i'll show you later.
the 65000 car depreciates at 8% per year, so the annual change in its value is 1 - .08 = .92
the formula for x years of depreciation would be 65,000 * .92^x.
the 25000 car appreciates at 5% per year, so the annual change in its value is 1 + .05 = 1.08
the formula for x year of appreciation would be 25,000 * 1.05^x
the break even point is when these 2 equations are equal to each other.
the equation for that is:
65,000 * .92^x = 25,000 * 1.05^x
divide both sides of this equation by 1.05^x and divide both sides of this equation by 65,000 to get:
.92^x / 1.05^x = 25,000 / 65,000
to solve this equation, take the log of both sides to get:
log [ .92^x / 1.05^x ] = log [ 25,000 / 65,000 ]
since log (a/b) = log(a) - log(b), your equation can becomes:
log (.92^x) - log(1.05^x) = log (25,000 / 65,000)
you don't need to change the right side of the equation because you can handle that expression as it is with your calculator.
since log(x^a) = a * log(x), this equation can now become:
x * log(.92) - x * log(1.05) = log (25,000 / 65,000)
you can factor out the x to get:
x * [ log(.92) - log(1.05) ] = log (25,000 / 65,000)
you can divide both sides of your equation by [ log(.92) - log(1.05 ] to get:
x = [ log(25,000 / 65,000) ] / [ log(.92) - log(1.05) ]
from here on out it's use your calculator to get the value of x.
i got:
x = 7.229315478
that's the number of years it will take for their values to be the same.
65,000 * .92^(7.229315478) = 35,573.29848
25,000 * 1.05^(7.229315478) = 35573.29848
if you want to see it on a graph, look below:
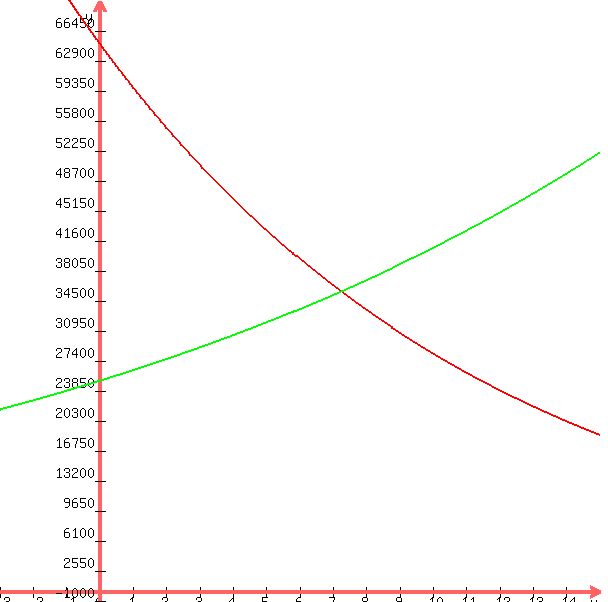
|
|
|