SOLUTION: One-third of the bigger of two consecutive odd numbers is 4 greater than one-fifth of smaller number. Find the numbers.

Smaller odd integer = n
Bigger odd integer = n+2

Replace the words "One-third of the bigger of two consecutive odd numbers"
by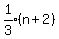 

Replace the word "is" by " = ".

Replace the words "4 greater than one-fifth of smaller number" by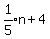 

So we have the equation

             = 

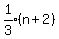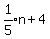Multiply through by LCD = 15

             5(n+2) = 3n + 60
            5n + 10 = 3n + 60
                 2n = 50
                  n = 25

So the smaller odd integer is n=25, and the larger one is n+2 = 25+2 = 27

Checking:

That's on-third of 27 which is 9

That's one-fifth of 25, which is 5.

And indeed 9 is 4 greater than 5.

So it checks.  Answer: 25 and 27

Edwin