Question 6682: Two planes start from the same airport and fly in opposite directions. The second plane starts one-half hour after the first plane, but its speed is 50 miles per hour faster. Find the ground speed of each plane if two hours after the first plane starts its flight the planes are 2000 miles apart.
Answer by prince_abubu(198)   (Show Source): (Show Source):
You can put this solution on YOUR website! We're going to use the formula rate * time = distance, but with a few twists.
If they're traveling in opposite directions, then their individual distances must add up, in this case, add upto 2000 miles. So  . .
Let's take care of the distance the first plane will travel. They didn't tell us the speed (or rate) of the first plane, so we'll call it  . Another fact that the problem provided for us is that the other plane left 1/2 hour later. The way to look at it is that this first plane had 1/2 an hour more to fly. So, the distance that the first plane traveled during the first half hour is . Another fact that the problem provided for us is that the other plane left 1/2 hour later. The way to look at it is that this first plane had 1/2 an hour more to fly. So, the distance that the first plane traveled during the first half hour is 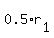 . So the plane must travel at its own speed for the rest of the time. The problem did say that the planes are going to be 2000 miles apart two hours after the first plane left. If the first plane flew alone for the first 1/2 hour, then there is to be 1.5 hours left until both planes are 2000 miles apart. So that's another distance of . So the plane must travel at its own speed for the rest of the time. The problem did say that the planes are going to be 2000 miles apart two hours after the first plane left. If the first plane flew alone for the first 1/2 hour, then there is to be 1.5 hours left until both planes are 2000 miles apart. So that's another distance of  . So, the total distance that plane #1 traveled is . So, the total distance that plane #1 traveled is 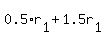 or actually or actually 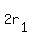 . In actuality, the plane did travel for the full two hours. . In actuality, the plane did travel for the full two hours.
The second plane's rate is said to be 50 miles per hour faster than the first plane. So, that's 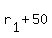 . If it took two hours for the plane to travel, and the first 1/2 hour of it was solo, then the next 1.5 hours is the time flying together. This means that plane#2 only flew for 1.5 hours. So, the distance that plane#2 travels is . If it took two hours for the plane to travel, and the first 1/2 hour of it was solo, then the next 1.5 hours is the time flying together. This means that plane#2 only flew for 1.5 hours. So, the distance that plane#2 travels is 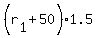
Now, let's add up the two planes' distances:

 <--- used distributive property to expand. <--- used distributive property to expand.
 <--- combined like terms <--- combined like terms

 <---- The first plane traveled at 550 miles per hour. If the second plane traveled 50 miles per hour faster, then it's speed would've been 600 miles per hour. <---- The first plane traveled at 550 miles per hour. If the second plane traveled 50 miles per hour faster, then it's speed would've been 600 miles per hour.
|
|
|