SOLUTION: A trough of length 6 m has a uniform cross section which is an equilateral triangle with sides 1 m. Water leaks from the bottom of the trough at a constant rate of 0.1 m^3 per minu

Algebra ->  Test -> SOLUTION: A trough of length 6 m has a uniform cross section which is an equilateral triangle with sides 1 m. Water leaks from the bottom of the trough at a constant rate of 0.1 m^3 per minu      Log On


   

Question 667241: A trough of length 6 m has a uniform cross section which is an equilateral triangle with sides 1 m. Water leaks from the bottom of the trough at a constant rate of 0.1 m^3 per minute. Find the rate at which the water level is falling at the instant when it is 20 cm deep?
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
A trough of length 6 m has a uniform cross section which is an equilateral triangle with sides 1 m. Water leaks from the bottom of the trough at a constant rate of 0.1 m^3 per minute. Find the rate at which the water level is falling at the instant when it is 20 cm deep?
This is a cross section of the trough.  The blue line is the water
level.  The red line h is the height of the water level.  We are
looking for the rate at which h is shrinking when h=20cm.   




The volume of the water is the area of the equilateral triangle
whose base is the blue line times the trough length of 6m, The
area of the triangle is 1%2F2(2x)(h) or xh and multiplying
this by the trough length of 6 m, we have

                      V = 6xh

We also know that h%2Fx = tan(60°) = Ö3.

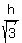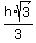So h%2Fx=sqrt%283%29%2F1, therefore x = h%2Fsqrt%283%29 = h%2Asqrt%283%29%2F3, so V = 6xh becomes 

                     V = 6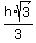h%2Asqrt%283%29%2F3h
or
                     V = 2·Ö3·h²

Differentiating with respect to time t

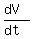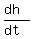                    %28dV%29%2F%28dt%29 = 4·Ö3·h·%28dh%29%2F%28dt%29 

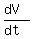We are given that %28dV%29%2F%28dt%29 = -0.1 m³ taken negative because the
volume of water is decreasing.  And we want the particular value of
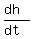%28dh%29%2F%28dt%29 when h = 20 cm = 0.2 m.

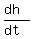                    -0.1 = 4·Ö3·0.2·%28dh%29%2F%28dt%29

Solve that for 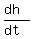%28dh%29%2F%28dt%29 and we get

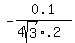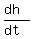                   -0.1%2F%284sqrt%283%29%2A.2%29 = %28dh%29%2F%28dt%29

Multiply top and bottom by 10

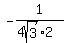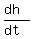
                   -1%2F%284sqrt%283%29%2A2%29 = %28dh%29%2F%28dt%29                   

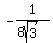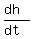                   -1%2F%288sqrt%283%29%29 = %28dh%29%2F%28dt%29

Rationalize the denominator:

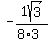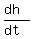
                   -1sqrt%283%29%2F%288%2A3%29 = %28dh%29%2F%28dt%29

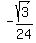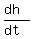                   -sqrt%283%29%2F24 = %28dh%29%2F%28dt%29

That's in meters/minute, so to change it to centimeters/minute,
multiply by 100

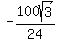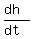
                   -100sqrt%283%29%2F24 = %28dh%29%2F%28dt%29

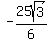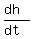                   -25sqrt%283%29%2F6 = %28dh%29%2F%28dt%29

which is about -7.2 centimeters/minute, which means that the water 
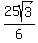level is falling at 25sqrt%283%29%2F6 centimeters/minute or 
about 7.2 centimeters/minute.

Edwin