Question 666327: What polynomial, when divided by 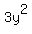 yields yields  as a quotient? as a quotient?
Answer by Leaf W.(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! The polynomial will be the product of what it is being divided by (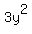 ) and the quotient ( ) and the quotient ( ). If you do not understand why, here is an example of a simpler problem that will hopefully make this idea easier: ). If you do not understand why, here is an example of a simpler problem that will hopefully make this idea easier:
6 / 2 = 3
The 6 is the number being divided, similar to the polynomial you are looking for in this problem. The 2 is the number the polynomial is divided by, similar to the 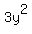 in your problem. Finally, the 3 is the quotient, similar to the in your problem. Finally, the 3 is the quotient, similar to the  in your problem. in your problem.
What I just said is that the polynomial (or in our simpler example, the 6) will be the product (multiplication) of what it is being divided by (the 2) and the quotient (the 3). If we do the math, we find out that this is correct:
2 * 3 = 6
If we try other examples, this still holds true:
8 / 4 = 2; 4 * 2 = 8
15 / 3 = 5; 3 * 5 = 15
Therefore, we can find the answer to the problem by multiplying 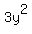 and and  . .
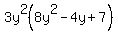
Distribute the 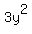 into the into the  by multiplying it by each element: by multiplying it by each element:
1. 
2. 
3. 
Therefore, the solution to your problem is  . .
|
|
|