SOLUTION: Train A leaves a station traveling at 25 mph. One half hour later Train B leaves the same station traveling the same direction at 35 mph. How does it take for Train B to catch up t

Without algebra (in your head):
When B starts, A is 12.5 miles down the track (half of 25).  B's catch-up 
rate is 35-25 or 10 mph.  In 1 hour B has caught up 10 of the 12.5 miles.
The remaining 2.5 miles is one quarter of 10 miles, so he'll need another
quarter of an hour or 15 minutes.   Answer: 1 hour 15 minutes.

With algebra:

Let t = train A's time. Train A's time is .5 hour more 
than train B's time, or t+.5 

           rate × time = distance
---------------------------------
Train A     25  × t+.5 = 25(t+.5) 
---------------------------------
Train B     35  ×  t   =    35t

Set the distances equal:

       25(t+.5) = 35t
       25t+12.5 = 35t
           12.5 = 10t
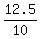            = t
           1.25 = t

1 hour and a quarter or 1 hour and 15 minutes.

Edwin