Question 662461: Question: In an arithmetic series of 50 terms, the 17th term is 53 and the 28th term is 86. Find the sum of the series.
Problem: I've gone through all the steps but I ended up with a different answer than what's in the back of my textbook. I'm going to type everything thing I did below, and hopefully someone can tell me where I messed up. I used \ when referring to division and / when referring to a fraction.
t17=53
t28=86
tn=a+(n-1)d
53=a+(17-1)d
53=a+16d
a=53-16d
Sn=n\2(2a+(n-1)d)
86=28/2(2a+(28-1)d)
86=14(2a+27d)
86=14(2(53-16d)+27d)
6/1/7=2(53-16d)+27d
6/1/7=106-32d+27d
-99/6/7=5d
-19/34/35=d
a=53-16(-19/34/35)
a=53-320
a=-267
Sn=n\2(2a+(n-1)d)
Sn= 50\2(2(-267)+(50-1)-19/34/35)
Sn=25(-534+(49)-19/34/34)
Sn=25(-1512/3/5)
Sn=-37815
The answer im the back of my textbook says it's suppose to be 3925
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first part of your work is right.
term number  is is  --> --> 
term number  is is 
 --> -->  <--> <--> 
You were on your way to finding  and and  . .
You just needed to use more data to get  and and  . .
Next, you misinterpreted "the 28th term is 86" (or maybe lost track of your planned steps)
You wrote  , the formula for sum of the first , the formula for sum of the first  terms, terms,
followed by  as if the sum of the first 28 terms was 86. as if the sum of the first 28 terms was 86.
You knew that the next step would require using that formula for the sum,
but lost track, and skipped a step.
At that point, a bunch of people would write some of this:
term number 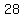 is is 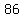 --> --> 
term number  is is 
 --> --> 
Then, they would use  , along with , along with  to find to find  and and  . .
They would write the system 
and would solve it to get  and and  . .
RANT:
I may write all that to go with the flow, and please a teacher,
but I prefer to use definitions, logic and 5th grader reasoning (if possible),
trying to always understand the meaning of my calculations,
rather than using formulas.
I look at it the fifth grader way:
Going from the 17th to the 28th term, we are adding  from one term to the next, from one term to the next,
and we do that  times, times,
so the difference between the 17th and the 28th terms must be  times times  . .
The difference is  , so I divide to get , so I divide to get 
Then, since you gave me  , ,
I use it to get  --> -->  --> -->  . .
THE SUM:

 --> -->  --> -->  --> -->  --> -->  . .
|
|
|