b²x² + 2ax = x² + a²
b²x² - x² + 2ax - a² = 0
(b²-1)x² + 2ax - a² = 0
We have to use the quadratic formula, but since the
quadratic formula contains the letters a and b, we
change the letters in the formula to capital letters:
x = 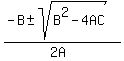 Then A = b²-1, B = 2a, C = -a²
x =
Then A = b²-1, B = 2a, C = -a²
x = 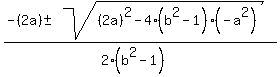 [Now we can see why they said "b does not equal 1" because the
denominator 2(b²-1) would be 0 if bcould equal 1, and we cannot
divide by 0].
x =
[Now we can see why they said "b does not equal 1" because the
denominator 2(b²-1) would be 0 if bcould equal 1, and we cannot
divide by 0].
x =  x =
x = 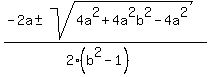 x =
x = 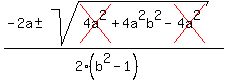 x =
x = 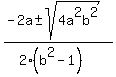 x =
x =  x =
x = 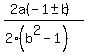 x =
x = 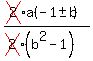 x =
x =  There are two solutions, one using the + and one using the -
Solution 1:
x =
There are two solutions, one using the + and one using the -
Solution 1:
x = 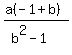 Reverse the terms in the parentheses in the numerator:
x =
Reverse the terms in the parentheses in the numerator:
x = 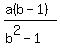 Factor the denominator:
x =
Factor the denominator:
x = 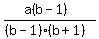 x =
x = 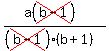 x =
x = 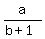 Solution 2:
x =
Solution 2:
x = 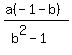 Reverse the terms in the parentheses in the numerator:
x =
Reverse the terms in the parentheses in the numerator:
x = 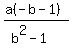 Factor -1 out of the parentheses in the numerator:
x =
Factor -1 out of the parentheses in the numerator:
x = 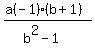 x =
x = 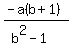 Factor the denominator:
x =
Factor the denominator:
x = 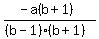 x =
x = 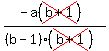 x =
x = 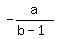 So the solutions are
So the solutions are 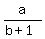 and
and 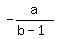 Edwin
Edwin