|
Question 662256: Im trying to help my sister with her hw yet i dont kno how to do this, would someone help me so i could teach her
Milk Problem: Handy Andy sells one-gallon cartons of milk (4 quarts) for $3.09 each and half-gallon cartons for $1.65 each. Assume that the number of cents you pay for a carton of milk varies linearly with the number of quarts the carton holds.
a) Write the particular equation expressing price in terms of quarts.
b) If Handy Andy sold 3-gallon cartons, what would your equation predict the price to be?
c) The actual prices for pint cartons (1/2 quart) and one-quart cartons are $.57 and $.99, respectively. Do these prices fit your mathematical model? If not, are they higher than predicted or lower?
d) Suppose that you found cartons of milk marked at $3.45, but that there was nothing on the carton to tell what size it is. According to your model, how much would such a carton hold?
e) What doe the price-intercept represent in the real world?
f) What are the units of the slope? What real-world quantity does this number represent?
g) Sketch and label the graph.
Found 2 solutions by KMST, mari_hernandez:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  = number of quarts
 = price in $
(Explanation: We have to start by defining variables that will be related by a linear equation. Next, we have to use the two (x,y) data points given to find the equation)
one gallon (4 quarts) for $3.09 --> (4,3.09) (x=4, y=3.09)
half gallon (2 quarts) for $1.65 --> (2,1.65) (x=2, y=1.65)
a) Write the particular equation expressing price in terms of quarts.
(Explanation: We are looking for an equation of the form  . We can substitute the (x,y) values for each data point to get a system of equation to solve for  and  . Otherwise, we can use the two points to calculate the slope of the line, and then we can find the rest of the equation one way or another)
Using a system of equations:
Subtracting the second equation from the first equation;
-
-----------------
 -->  --> 
Substituting that value in the second equation, we get
 -->  -->  --> 
The equation is 
Using slope:
(Explanation: the slope, in the change in y divided by the change in x, as we go from one data point to the other.)
 -->  -->
The point-slope form of the equation, using point (2,1.65), is:
-->  -->  -->
b) If Handy Andy sold 3-gallon cartons, what would your equation predict the price to be?
Substituting  in the equation, we get
 -->  --> 
Andy would sell a 3-gallon carton for $8.85.
c) The actual prices for pint cartons (1/2 quart) and one-quart cartons are $.57 and $.99, respectively. Do these prices fit your mathematical model? If not, are they higher than predicted or lower?
The predictions are found using the equation 
For 1/2 qua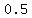rt =  quart,  , so
 -->  --> 
For 1 quart,  , so
 -->  --> 
the price for pint cartons agrees with the  prediction,
but the price for the quart, $0.99, is higher than the  prediction.
d) Suppose that you found cartons of milk marked at $3.45, but that there was nothing on the carton to tell what size it is. According to your model, how much would such a carton hold?
I would use  and the equation to find the number of quarts, .
 -->  -->  -->  --> 
Such a carton would hold 4.5 quarts according to the model.
e) What does the price-intercept represent in the real world?
The price-intercept is the y-intercept in the equation .
It is the value, 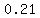 , representing $0.21, the price of a carton with zero quarts of milk inside. It represents the cost of the carton plus maybe Andy's work making a sale.
f) What are the units of the slope? What real-world quantity does this number represent?
The slope, 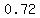 , represents the cost of the milk per quart.
The units are $/quart, and it gets multiplied by the number of quarts to find the price of the milk inside the carton in $.
g) Sketch and label the graph.
 To graph, we just need to plot 2 points (blue circles) and connect then with a line.
The blue line represents .
The blue circles represent
the intercept point, (0,0.21),  with  , and
point (4,3.09),  with  , representing 4 quarts at $3.09.
Answer by mari_hernandez(1)  (Show Source):
You can put this solution on YOUR website! = number of quarts
= price in $
(Explanation: We have to start by defining variables that will be related by a linear equation. Next, we have to use the two (x,y) data points given to find the equation)
one gallon (4 quarts) for $3.09 --> (4,3.09) (x=4, y=3.09)
half gallon (2 quarts) for $1.65 --> (2,1.65) (x=2, y=1.65)
a) Write the particular equation expressing price in terms of quarts.
(Explanation: We are looking for an equation of the form . We can substitute the (x,y) values for each data point to get a system of equation to solve for and . Otherwise, we can use the two points to calculate the slope of the line, and then we can find the rest of the equation one way or another)
Using a system of equations:
Subtracting the second equation from the first equation;
-
-----------------
--> -->
Substituting that value in the second equation, we get
--> --> -->
The equation is
Using slope:
(Explanation: the slope, in the change in y divided by the change in x, as we go from one data point to the other.)
--> -->
The point-slope form of the equation, using point (2,1.65), is:
--> --> -->
b) If Handy Andy sold 3-gallon cartons, what would your equation predict the price to be?
Substituting in the equation, we get
--> -->
Andy would sell a 3-gallon carton for $8.85.
c) The actual prices for pint cartons (1/2 quart) and one-quart cartons are $.57 and $.99, respectively. Do these prices fit your mathematical model? If not, are they higher than predicted or lower?
The predictions are found using the equation
For 1/2 quart = quart, , so
--> -->
For 1 quart, , so
--> -->
the price for pint cartons agrees with the prediction,
but the price for the quart, $0.99, is higher than the prediction.
d)
I would use and the equation to find the number of quarts, .
a carton would hold 4.5 quarts according to the model.
e)
The price-intercept is the y-intercept in the equation .
It is the value, , representing $0.21, the price of a carton with zero quarts of milk inside. It represents the cost of the carton plus maybe Andy's work making a sale.
f) What are the units of the slope? What real-world quantity does this number represent?
The slope, , represents the cost of the milk per quart.
The units are $/quart, and it gets multiplied by the number of quarts to find the price of the milk inside the carton in $.
|
|
|
| |
