Question 662237: State the relation shown by each of the following mappings.then state if the relation is a function.
D R
8 3
-1 3
2 3
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! first see if the given points lie on same line:
| Solved by pluggable solver: To determine if 3 points lie in a line |
The 3 points lie on a same plane. For all points to lie on a line they should satisfy the equation of a line. Hence any two points taken on a line should calculate to the same slope of a line.
In order to prove the 3 points to lie on a line, as there exists a unique line containing three points and every line has a unique slope.
Hence it will be sufficient to prove that the slope calculated taking 2 points at a time should be equal.
Slope of line taking points (X1,Y1) and (X2,Y2) is

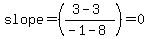 ........................(1) ........................(1)
Slope of line taking points (X3,Y3) and (X1,Y1) is

 ........................(2) ........................(2)
From conditions (1) and (2)
The slopes are equal hence the 3 points can lie on same line.
If the slope calculated from points (X2,Y2) and (X3,Y3) comes out to be same then it is confirmed that the 3 points lie on a same line.

 ........................(3) ........................(3)
From (1),(2) and (3)
Hence, It is proved that the 3 points lie on same line.
To read more on equations of a line refer to articles on wikipedia
|
now, find the equation of line going through two of given points:
| Solved by pluggable solver: FIND EQUATION of straight line given 2 points |
hahaWe are trying to find equation of form y=ax+b, where a is slope, and b is intercept, which passes through points (x1, y1) = (8, 3) and (x2, y2) = (-1, 3).
Slope a is  . .
Intercept is found from equation  , or , or  . From that, . From that,
intercept b is  , or , or  . .
y=(0)x + (3)
Your graph:

|
as you can see, the line is parallel to  and it is a function called a and it is a function called a 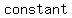  , because to every value of , because to every value of there corresponds the same value of there corresponds the same value of (in this case (in this case  for all for all  ) )
|
|
|