Question 661979: The yearly production of a 5 foot orange tree is 35 pounds of oranges. A 12 foot tree produces 54 pounds.
What is the predicted production of an 18 foot tree?
What is the predicted production of an 20 foot tree?
What is the predicted height ( in feet ) of a tree that produces 88 pounds of oranges?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the production,  of an orange tree varies linearly with its height, of an orange tree varies linearly with its height,  , ,
we can write the linear equation that describes it, knowing two ( , , ) points. ) points.
"The yearly production of a 5 foot orange tree is 35 pounds of oranges," gives us point ( , , ). ).
"A 12 foot tree produces 54 pounds," gives us point ( , , ). ).
I can see 3 ways to get the answer.
The expected way to solve the problem depends on what you are studying in class.
CALCULATING SLOPE OF A LINE AND WRITING THE POINT-SLOPE FORM:
We can calculate the slope,  of the line: of the line:
 --> -->  . .
Then we can use that slope and the coordinates of one of the points to write the equation in point-slope form.

From the point-slope form, we can go to the slope-intercept form, which will help answer the first 2 questions:
 --> --> --> --> --> --> --> --> --> -->
With a calculator, we can use the approximation 
and get accurate enough results.
I'll stick with the fractions just in case you are expected to do that.
For the 18 foot tree,  , so , so
 --> --> --> --> =about =about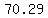 =about =about (rounding) (rounding)
I assume the expected answer is 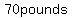 rounding to whole numbers. rounding to whole numbers.
For the 20 foot tree,
 --> -->  --> --> --> --> =about =about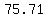 =about =about (rounding) (rounding)
I assume the expected answer is 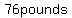 rounding to whole numbers. rounding to whole numbers.
For the 88 pound production,  , so , so
 --> --> --> --> --> -->
Multiplying both sides times  : :
 --> --> --> --> =about =about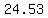 =about =about (rounding) (rounding)
I assume the expected answer is 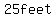 rounding to whole numbers. rounding to whole numbers.
SETTING UP A SYSTEM OF EQUATIONS TO FIND SLOPE AND INTERCEPT:
WE can find an equation of the form 
by substituting the coordinates for out 2 points and solving the system

Solving the system of equations leads to
 =about =about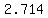 (rounding) (rounding)
and  =about =about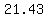 (rounding) (rounding)
From that point on, the calculations are the same as done above.
USING A COMPUTER/CALCULATOR AS IF IT IS A STATISTICS PROBLEM
Using Excel functions in my computer, I can answer all 3 questions.
With A1=5, A2=12, B1=35, B2=54,
=FORECAST(18,B1:B2,A1:A2) gives me 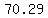 or or 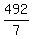 or or 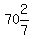 pounds of oranges for an 18 foot tree. pounds of oranges for an 18 foot tree.
=FORECAST(20,B1:B2,A1:A2) gives me 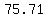 or or 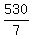 or or 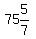 pounds of oranges for an 20 foot tree. pounds of oranges for an 20 foot tree.
=FORECAST(88,A1:A2,B1:B2) gives me 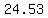 feet for the height of a tree that would produce 88 pounds of oranges in a year. feet for the height of a tree that would produce 88 pounds of oranges in a year.
|
|
|