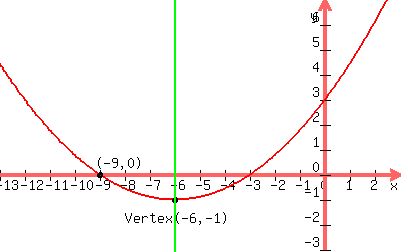
Since -9 is a root, it has an x-intercept of (-9,0)
We plot those given points:
 We know that the axis of symmetry is a vertical line through
the vertex:
that goes through the vertex. So we draw that:
We know that the axis of symmetry is a vertical line through
the vertex:
that goes through the vertex. So we draw that:
 And we can sketch in the parabola so that the green line
bisects it:
And we can sketch in the parabola so that the green line
bisects it:
 All quadratic functions have the equation
y = a(x - h)² + k
where the vertex is (h,k). In this case (h,k) = (-6,-1), so the
equation is
y = a(x - (-6))² + (-1), or upon simplifying,
y = a(x + 6)² - 1
We only need the value of a.
It goes through (-9,0) so we substitute x=-9 and y=0
y = a(x + 6)² - 1
0 = a(-9 + 6)² - 1
0 = a(-3)² - 1
0 = a(9) - 1
0 = 9a - 1
1 = 9a
All quadratic functions have the equation
y = a(x - h)² + k
where the vertex is (h,k). In this case (h,k) = (-6,-1), so the
equation is
y = a(x - (-6))² + (-1), or upon simplifying,
y = a(x + 6)² - 1
We only need the value of a.
It goes through (-9,0) so we substitute x=-9 and y=0
y = a(x + 6)² - 1
0 = a(-9 + 6)² - 1
0 = a(-3)² - 1
0 = a(9) - 1
0 = 9a - 1
1 = 9a
 = a
So the equation is
y =
= a
So the equation is
y =  (x + 6)² - 1
You can leave it like that or you can continue:
y =
(x + 6)² - 1
You can leave it like that or you can continue:
y =  (x + 6)(x + 6) - 1
y =
(x + 6)(x + 6) - 1
y =  (x² + 12x + 36) - 1
y =
(x² + 12x + 36) - 1
y =  (x² + 12x + 36) -
(x² + 12x + 36) -  y =
y =  -
-  y =
y = 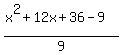 y =
y =  From there you can either factor the numerator
and leave it like this:
y =
From there you can either factor the numerator
and leave it like this:
y = 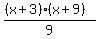 Or you can take this:
y =
Or you can take this:
y =  write it as
y =
write it as
y = 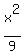 +
+ 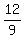 x +
x +  and then as
y =
and then as
y =  x² +
x² +  x + 3
Edwin
x + 3
Edwin