Question 65956: The length of a rectangular playing field is 5 ft less than twice its width.
If the perimeter of the playing field is 230 ft, find the length and width of the field.
Answer by chitra(359)  (Show Source): (Show Source):
You can put this solution on YOUR website! Let "l" be the lenght of the field
and
"b" be the breadth of the rectangular field.
Given that the perimeter of the field is 230ft.
Also, given that the lenght of the field is 5ft less than twice its width.
Therefore,
l = 2b - 5 and b = b
The perimeter is given by 2l + 2b
Hence, 2l + 2b = 230
2(2b - 5) + 2b = 230
4b - 10 + 2b = 230
Adding like terms, we get:
6b - 10 = 230
6b = 230 + 10
6b = 240
b = 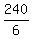
==> b = 40
Now, substitute this value in the equation for l. We get:
l = 2b - 5
l = 2(40) - 5
l = 80 - 5
l = 75
Hence, the solution.
|
|
|