SOLUTION: from 2 point south of a hill on a level ground and are 1000ft apart, the angels of elevation of the hill are 12º20' and 82º40'. how high is the hill?

The following depicts the situation.  (The figure is not drawn to scale.)



The two small circles indicate the two points on level ground
which are 1000 feet apart.  We want to find y, the height of 
the hill.

There are two right triangles involved here. They are these:

and

In the first right triangle the side opposite the 12°20' angle is y,
and the side adjacent the 12°20' is 1000+x, so using the fact that
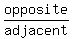tangent =  we have the equation
from the first right triangle:

tan(12°80') =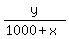 

In the second right triangle the side opposite the 82°40' angle is y,
and the side adjacent the 82°40' is x, so again using the fact that
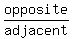tangent =  we have the equation
from the second triangle:

tan(82°40') = 

To keep from getting bogged down in notation,
since those tangents are bulky to write let's let

A = tan(12°20') and B = tan(82°40')

Then the equations look simpler as:

A =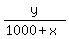  
B = 

Multiplying both through by their denominators:

A(1000+x) = y
       Bx = y

We want y, not x, so we solve for x.
Solving the second equation for x:

        x =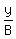 

Substituting in the first equation:

A(1000+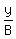) = y

Distribute:

1000A +  = y

Multiply through by B

1000AB + Ay = By

Get both terms in y on the right side:

1000AB = By - Ay

Factor out y on the right

1000AB = y(B - A)

Divide both sides by (B - A)

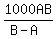 = y

Now substitute A = tan(12°20') and B = tan(82°40') 

 = y

That works out to be 224.9752003 or 
the hill is about 225 feet high.

Edwin