Question 658654: find the number of ways of selecting four letters from the word 'EXAMINATION'.ANSWER IS 136 PLS SOLVE THIS THANK U
Found 2 solutions by MathLover1, kevwill:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! EXAMINATION has  letters, and in which ' letters, and in which ' ', ' ', ' ' and ' ' and ' ', all occur twice. ', all occur twice. 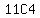 , would have been fine if all letters were distinct. , would have been fine if all letters were distinct.
So, we have , ,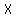 , ,  , ,  , ,  , ( , (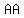 ), ( ), (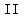 ), ( ), ( )... )...  distinct letters. distinct letters.
1.  letters selected, which are letters selected, which are  distinct: distinct: 
2.  letters alike, and letters alike, and  distinct (eg: distinct (eg: 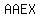 ) = ) =
3.  letters alike, and letters alike, and  letters alike (eg: letters alike (eg: 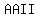 ) = ) = 
So answer is, . .
Answer by kevwill(135)   (Show Source): (Show Source):
You can put this solution on YOUR website! Actually, the answer is 131.
For an excellent, detailed description of the theory behind the solution, please see http://mathforum.org/library/drmath/view/56197.html
I sorted the letters of the word EXAMINATION by frequency of occurrence to get AAIINNEMOTX. That told me we are looking for the number of 4-combinations of the set (2,2,2,1,1,1,1,1).
We can use the generating function  and find the coefficient of the resulting and find the coefficient of the resulting  term. term.
When multiplied out, the expanded generating function is:
 and the coefficient of the and the coefficient of the  term is 131. Thus, there are 131 ways to select four letters from the word "EXAMINATION" term is 131. Thus, there are 131 ways to select four letters from the word "EXAMINATION"
|
|
|