|
Question 65860:
Hi, I'm having a difficult time figuring this problem
out. THANKS FOR HELPING!!
Find the longest and shortest line segment drawn in
the following diagram.
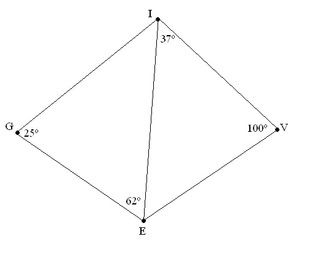
Found 2 solutions by ptaylor, Edwin McCravy:
Answer by ptaylor(2198)   (Show Source):
You can put this solution on YOUR website! Since you only specify angles in this polygon and we don't know the length of any side, I submit that any side can be infinitely long. Also, it's noteworthy that angle(GIE) is 93 degrees which makes the drawing somewhat off scale.
An interesting problem----I would like to know the source document for this problem.
Hope this helps----ptaylor
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
Hi, I'm having a difficult time figuring this problem
out. THANKS FOR HELPING!!
Find the longest and shortest line segment drawn in
the following diagram.
The sides of a triangle are always in the same order
of size as the angles opposite them:
First we calculate the two angles we aren't given by
using the fact that the three angles of any triangle
must always have sum 180°
ÐG + ÐEIG + ÐGEI = 180°
25° + ÐEIG + 62° = 180°
87° + ÐEIG = 180°
ÐEIG = 93°
ÐV + ÐEIV + ÐIEV = 180°
100° + 37° + ÐIEV = 180°
137° + ÐIEV = 180°
ÐIEV = 43°
In DEGI, ÐG < ÐGEI < ÐEIG, so their opposite sides
are respectively in the same order:
EI < GI < EG
In DEIV, ÐEIV < ÐIEV < ÐV, so their opposite sides
are respectively in the same order:
EV < IV < EI
So we can put those two inequalities together, and
get
EV < IV < EI < GI < EG
Therefore EV is the shortest side and EG is the
longest side.
Edwin
|
|
|
| |
