SOLUTION: if 7 cards are dealt from an ordinary desk of 52 playing cards , what is the probability that (a) at least 1 of them will be a queen?

Algebra ->  Probability-and-statistics -> SOLUTION: if 7 cards are dealt from an ordinary desk of 52 playing cards , what is the probability that (a) at least 1 of them will be a queen?      Log On


   

Question 658484: if 7 cards are dealt from an ordinary desk of 52 playing cards , what is the probability that
(a) at least 1 of them will be a queen?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
When you see "at least one", this means to find the probability
of the complement event, which is "none at all" and then subtract 
that probability from 1.

So we first work this problem:

If 7 cards are dealt from an ordinary desk of 52 playing cards, 
what is the probability that NONE OF THEM will be a queen?

That is the probability of selecting 7 of the 48 non-queens.

The numerator of that probability is "48 Choose 7" or C(48,7)
The denominator of that probability is "52 Choose 7" or C(52,7)

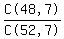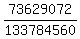%22C%2848%2C7%29%22%2F%22C%2852%2C7%29%22 = 73629072%2F133784560 ≈ .5504

So the probability you want is ≈ 1 - .5504 = .4496

Edwin