Question 65834: Hi, I had this problem for homework and I couldn't get it. THANKS FOR HELPING!!
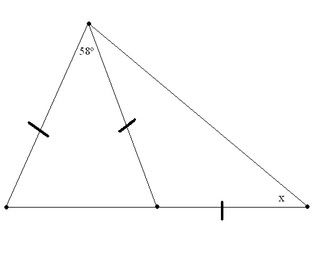
Find X.
Found 3 solutions by Earlsdon, Cintchr, stanbon:
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Using the well-known fact that in any plane triangle the sum of the three angles is 180 degrees. Let's find the two base angles of the isosceles triangle on the left side of your diagram.
In any isosceles triangle, the two base angles are equal, and the sum of the three angles (the two base angles and the vertex angle) in this triangle is 180 degrees. Let y = the measure of one of the base angles, then we can write:
58 + y + y = 180 Simplifying this, we get:
58 + 2y = 180 Subtracting 58 from both sides, we get:
2y = 122 Finally, dividing by 2, we have:
y = 61 degrees.
Now that we know the measure of two base angles of the isosceles triangle, we can find the the measure of the other base angle of the isosceles triangle on the right. Let's call that one angle z.
We know that angle y and angle z are supplementary angles and their sum is 180 degrees.
This allows us to find angle z as follows:
y + z = 180 But angle y = 61 degrees, so substitute this for y:
61 + z = 180 Subtract 61 from both sides.
z = 119 degrees.
Using the fact that in an isosceles triangle, the base angles are equal, we know that one of the base angles is x degrees so the other one must x degrees also. Again, we know that the sum of the angles in a plane triangle is 180 degrees. So, we can write:
61 + x + x = 180 Subtracting 61 from both sides, we get:
2x = 119 Dividing by 2 we find that:
x = 59.5 degrees.
Answer by Cintchr(481)   (Show Source): (Show Source):
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! It would help to label the vertices of the outer triangle.
Start on the left side and go clockwise to mark angles A,B,C.
C is at the top.
There are two isosceles triangles: one on the left, one on the right.
The left has an apex angle of 58.
Each base angle in the left isosceles triangle is (1/2)(180-58)=61 degrees.
The point situated between C and A has two angles at it: one is a 61 degree
base angle; the other is the supplement of 61 which is 180-61=119 degrees.
Then each of the base angles of the RIGHT isosceles triangle is (1/2)(180-119)
=30.5 degrees
One of those base angles is x.
So x=30.5 degrees
Cheers,
Stan H.
|
|
|