SOLUTION: Find the three consecutive integers such that four times the square of the third, less than three times the square of the first, minus 41, is twice the square of the second

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: Find the three consecutive integers such that four times the square of the third, less than three times the square of the first, minus 41, is twice the square of the second      Log On


   

Question 657991: Find the three consecutive integers such that four times the square of the third, less than three times the square of the first, minus 41, is twice the square of the second
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

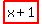three consecutive integers highlight%28x%29,highlight%28x%2B1%29 & highlight%28x%2B2%29

 such that four times the square of the third, less than three times the square of the first, 

minus 41, is twice the square of the second

Question states***

 4(x+2)^2 - 3x^2 - 41 = 2(x+1)^2

 4(x^2 + 4x + 4) - 3x^2 - 41 = 2(x^2 + 2x+ 1)

 4x^2 + 16x + 16 - 3x^2 - 41 = 2x^2 + 4x + 2

                0 = x^2 - 12x + 27

                0 = (x-9)(x-3)

                  x = 9  0r x = 3

Integers are 9, 10, 11

0r  3,4,5