SOLUTION: Determine the value(s) of the variable that must be excluded from the domain. f(x) = {{{x^2 - 16)/(-9x^2 + 27x + 36)}}}

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Determine the value(s) of the variable that must be excluded from the domain. f(x) = {{{x^2 - 16)/(-9x^2 + 27x + 36)}}}       Log On


   

Question 656250: Determine the value(s) of the variable that must be excluded from the domain.
f(x) = x%5E2+-+16%29%2F%28-9x%5E2+%2B+27x+%2B+36%29


Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
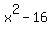f(x) = x%5E2+-+16%29%2F%28-9x2+%2B+27x+%2B+36%29

The denominator must not be 0

-9x² + 27x + 36 ≠ 0

-9(x² - 3x - 4) ≠ 0

   -9(x-4)(x+1) ≠ 0

   x - 4 ≠ 0;  x + 1 ≠ 0
       x ≠ 4;      x ≠ -1

 The graph looks like this:



There is no point where x=-1 because there is a vertical 
asymptote there, and there is a hole in the curve, and
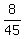therefore no point at (4,-8%2F45), where the little circle is.
So -1 and 4 are excluded from the domain.

The domain is

(-infinity,-1) U (-1,4) U (4,infinity)

Edwin