SOLUTION: What are the x-intercepts of the parabola whose equation is y = x² + 3x - 1

We can get points on the parabola, say these 6, 
by substituting x=-4, x=-3, x=-2, x=-1, x=0, x=1

(-4,3), (-3,-1), (-2,-3), (-1,-3), (0,-1), (1,3),  

 

We sketch in the parabola:



We want to know where this parabola crosses the x-axis, which I
have marked below with red circles:



From the graph it looks like the x-intercept on the left crosses somewhere
between -3 and -4, and the x-intercept on the right crosses somewhere
between 0 and 1.

To get these accurately we use the quadratic formula to find the values
of x that cause y to be 0:

The solution to

ax² + bx + c = 0

is found by:



Your problem is 

x² + 3x - 1 = 0

So a=1, b=3, c=-1







Use a calculator with the +

 = 0.3027756377, which is the x-coordinate
of the point circled on the right, and it is between 0 and 1.  So
that x-intercept on the right is

(0.3027756377, 0)

Use a calculator with the -

 = -3.302775638, which is the x-coordinate
of the point circled on the left, and it is between -3 and -4.  So
that x-intercept on the left is

(-3.302775638, 0)

Or you can write them in radical (exact) form:

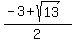(, 0) and (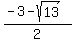, 0)

 Edwin