Since x³ has factors x³, x², and x we must include a
fraction with each of these as a denominator:
= 
+ 
+ 
+ 
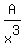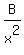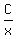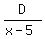Clear of fractions:
3x³ - 5x² - 3x + 15 = A(x-5) + Bx(x-5) + Cx²(x-5) + Dx³
Substitute x = 0 to eliminate the last three terms on the right:
3·0³ - 5·0² - 3·0 + 15 = A(0-5) + B·0(0-5) + C·0²(0-5) + D·0³
15 = -5A
-3 = A
Substitute that:
3x³ - 5x² - 3x + 15 = -3(x-5) + Bx(x-5) + Cx²(x-5) + Dx³
Substitute x = 5 to eliminate the first three terms on the right:
3·5³ - 5·5² - 3·5 + 15 = -3(5-5) + B·5(5-5) + C·5²(5-5) + D·5³
3·125 - 5·25 - 15 + 15 = -3(0) + B·5(0) + C·5²(0) + D·125
250 = 125D
2 = D
Substitute that:
3x³ - 5x² - 3x + 15 = -3(x-5) + Bx(x-5) + Cx²(x-5) + 2x³
Now that we have substituted all possible numbers that will eliminate
terms, we now substitute any other convenient numbers which WON'T
eliminate terms, but which will give us equations in the letters we
haven't determined. We haven't substituted 1, so let's choose x = 1:
Substitute x = 1
3·0³ - 5·0² - 3·0 + 15 = A(0-5) + B·0(0-5) + C·0²(0-5) + D·0³
3·1³ - 5·1² - 3·1 + 15 = -3(1-5) + B·1(1-5) + C·1²(1-5) + 2·1³
3 - 5 - 3 + 15 = -3(-4) + B(-4) + C(1-5) + 2
10 = 12 - 4B - 4C + 2
10 = 14 - 4B - 4C
4B + 4C = 4
Divide through by 4
B + C = 1
We haven't substituted 2, so let's substitute x = 2:
3·2³ - 5·2² - 3·2 + 15 = -3(2-5) + B·2(2-5) + C·2²(2-5) + 2·2³
3·8 - 5·4 - 6 + 15 = -3(-3) + B·2(-3) + C·4(-3) + 2·8
24 - 20 - 6 + 15 = 9 - 6B - 12C + 16
13 = 25 - 6B - 12C
6B + 12C = 12
Divide through by 6
B + 2C = 2
Solve the resulting system of equations by substitution or elimination
B + C = 1
B + 2C = 2
Get B = 0, C = 1
So we have A = -3, B = 0, C = 1, D = 2
Answer:
= + + +
= 
+ 
+ 
+ 
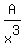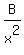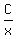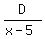
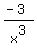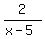Omitting the 0 term and bringing the negative sign out front of the
first term:
= —
+ +
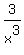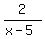Edwin
