Question 652123: what polygon has a number of sides that is five times the number of diagonals
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The way I understand geometry, the answer is  .
I am betting there is a mix-up in the wording of the problem.
The way I understand geometry,
a diagonal of a polygon is a segment that connects two vertices of the polygon, but is not a side of the polygon.
If a polygon has  sides, it will have n vertices.
Each vertex will be connected to  other vertices by sides,
and can be connected to the remaining  other vertices by a diagonal.
If we multiply the diagonals coming out of each vertex times , the number of vertices,
we get  ,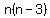
but we are counting each diagonal twice.
The polygon with sides has  diagonals.
To find what polygon has a number of sides that is five times the number of diagonals, we can set up an equation
or we can make a table comparing and  .
For that table:
A triangle has  sides and  diagonals.
A quadrilateral has  sides and diagonals.
From then on, the number of sides is equal to or less than the number of diagonals.
A pentagon has  sides and diagonals.
A hexagon has  sides and  diagonals.
Either way (equation or table), the answer is .
If we wanted to know what polygon has a number of diagonals that is five times the number of sides, our equation would be
-->  -->  -->  -->  --> 
Since  does not make a polygon, we know is not .
-->  -->  or  .
|
|
|
