Question 651783: I have had this problem for a month and I can't figure out what to do.
Maybe you can help.
A farmer is taking her eggs to the market in a cart, but she hits a
pothole, which knocks over all the containers of eggs. Though she is
unhurt, every egg is broken. So she goes to her insurance agent, who
asks her how many eggs she had. She says she doesn't know, but she
remembers somethings from various ways she tried packing the eggs.
When she put the eggs in groups of two, three, four, five, and six
there was one egg left over, but when she put them in groups of seven
they ended up in complete groups with no eggs left over.
What can the farmer figure from this information about the number of
eggs she had? Is there more than one answer?
I have already tried multiples of seven, but I can't figure the
answer out. Could you please tell me how to get the answer and also
tell me what it is?
Thanks for your help.
Found 2 solutions by MathLover1, stanbon:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If there were  eggs eggs 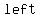 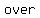 when put into groups of when put into groups of 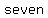 there there 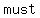 have been a have been a 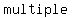 of of  eggs. eggs.
We need to find  where where




where  , ,  , ,  , and , and 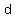 are the number of are the number of 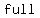 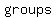 when the eggs are put into groups of when the eggs are put into groups of  , ,  , ,  , and , and  . .
 there is there is 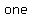 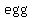  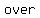 when the eggs are put into groups of when the eggs are put into groups of  there will automatically be there will automatically be 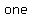 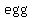  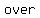 when they are put into groups of when they are put into groups of  or groups of or groups of  . So we can forget groups of . So we can forget groups of  and and  . .
The 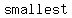 number which is number which is 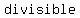 by by  and and  is is  , but , but  isn't divisible by isn't divisible by  , so the smallest number which will divide by , so the smallest number which will divide by  , ,  , and , and  is is  . .
So we need

but also

The easiest way to solve this is to try values  , , , ,  , , , ,  ,... for ,... for  to get values of to get values of 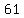 , ,  , , 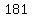 , , 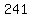 , , 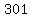 ... for ... for  , and to pick the first of these which divides by , and to pick the first of these which divides by  . This is . This is  . .
So the 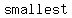 number of eggs is number of eggs is  . .
Adding 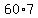 to a valid solution will also give a valid solution. to a valid solution will also give a valid solution.
So the next solution is  . .
All the solutions are  , , 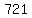 , , 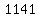 , , 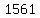 , , 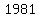 , ... (i.e. add , ... (i.e. add  each time) each time)
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! When she put the eggs in groups of two, three, four, five, and six
there was one egg left over, but when she put them in groups of seven
they ended up in complete groups with no eggs left over.
------
Equations:
(x-1)/2 = y1
----
(x-1)/3 = y2
------
(x-1)/4 = y3
----
(x-1)/5 = y4
-----
(x-1)/6 = y5
------
x/7 = y6
-----------
I used a TI-84 and looked for the x value that gave
an integer solution for all of the above equations.
---------------------------
Ans: x = 301 eggs
=======================
Cheers,
Stan H.
=======================
|
|
|