Question 651552: at 6AM, a boy rides his bike due north from campus at 12 mph. Two hours later, another boy rides his bike due east from the same point, also at 12mph. When will they be 120 miles apart?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! at 6AM, a boy rides his bike due north from campus at 12 mph.
Two hours later, another boy rides his bike due east from the same point, also at 12mph.
When will they be 120 miles apart?
:
let t = travel time of the 1st boy
then
(t-2) = travel time of the 2nd (left 2 hrs later)
therefore:
12t = distance traveled by the 1st boy
and
12(t-2) = (12t-24) = distance traveled by the 2nd
:
This is a pythag problem; a^2 + b^2 = c^2, where
a = 12t
b = 12(t-2)
c = 120
:
(12t)^2 + (12t-24)^2 = 120^2
:
144t^2 + 144t^2 - 288t - 288t + 576 = 14400
:
288t^2 - 576t + 576 - 14400 = 0
:
288t^2 - 576t - 13824 = 0
Simplify, divide thru by 288, results:
t^2 - 2t - 48 = 0
factors to
(t-8)(t+6) = 0
The positive solution
t = 8 hrs is the travel time of the 1st boy,
therefore
6:00 Am + 8:00 = 2:00 pm, they will 120 mi apart
:
:
Check this on your calc: enter 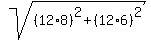
|
|
|