SOLUTION: If f(x) = 2x, describe the transformation of the curve for g(x) = -2 x-2 I desparetely need help with this thank you

Algebra ->  Graphs -> SOLUTION: If f(x) = 2x, describe the transformation of the curve for g(x) = -2 x-2 I desparetely need help with this thank you      Log On


   

Question 64826: If f(x) = 2x, describe the transformation of the curve for g(x) = -2 x-2
I desparetely need help with this thank you
Answer by mszlmb(115) About Me  (Show Source):
You can put this solution on YOUR website!
"If f(x) = 2x, describe the transformation of the curve for g(x) = -2 x-2
I desparetely need help with this thank you"

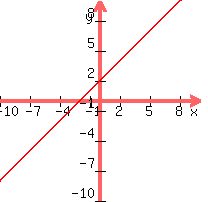
I assume you mean the line rather than the 'curve,' as both f(x) and g(x) are linear. For the record, here is a graph of both:

F(x)=2x
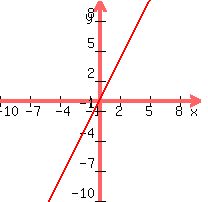
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2C2x%29
G(x)=-2x-2
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2C-2x-2%29


What the question is basically asking is 'How does G differ from F?'

To get from F to G, first we make the "2x" negative. What happens when you make something negative? They are 'flipped' along the horizontal axis. Here are some examples:
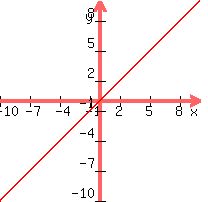
Graph of F(x)=x
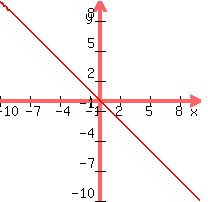
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2Cx%29
Graph of F(x)=-x
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2C-x%29

See how they're flipped along the horizontal (x) axis? Let's look at another:
Graph of F(x)=x/2
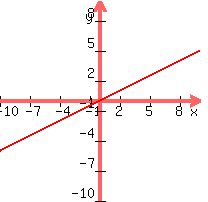
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2Cx%2F2%29
Graph of F(x)=-x/2
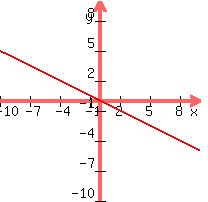
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2C-x%2F2%29


So, the graph of -2x in regard to 2x, is flipped;
Graph of F(x)=2x
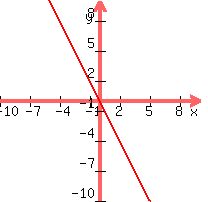
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2C2x%29
Graph of F(x)=-2x
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2C-2x%29


But then we subtract two, what does that do to the graph?? Here are some examples to help verify. Adding or subtracting to a linear equation (an equation in the form of y=mx+b) moves it along the vertical (y) axis:
Graph of F(x)=x
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2Cx%29
Graph of F(x)=x+2
graph%28200%2C200%2C-10%2C10%2C-10%2C10%2Cx%2B2%29

You know, let's have some fun with this. Following is a graph of the function Y=X+1, y=x+2, y=x+3, etc., and y=x+0, y=x-1, y=x-2, etc. Just to illustrate the point; these are all on the same graph: [EDIT: Upon reviewing, I found that many of the lines are white. They're plotted, but they're white. They'll look like cutouts of the x and y axes.]

Pretty cool, huh? You see, adding any amount to x moves it up that amount, and subtracting an amount from x moves it down that amount. Therefore, the difference between f(x)=2x and g(x)=2x-2 is that G(x) moves down two. Notice I didn't include g(x)=-2x-2.
Well, making it negative flips it along the x axis (horizontally), and subtracting 2 from it moves it down two units. Thus, the transformation is the line is flipped along the x axis and moved two units down.
Here are the anticipated graphs:
F(x)=2x
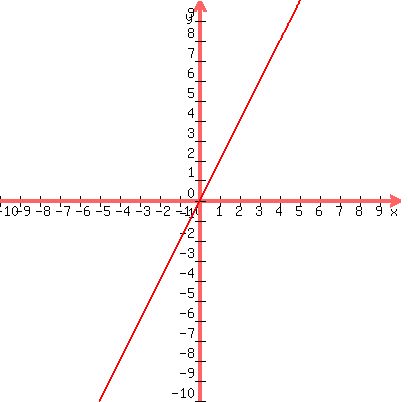
graph%28400%2C400%2C-10%2C10%2C-10%2C10%2C2x%29
G(x)=-2x-2
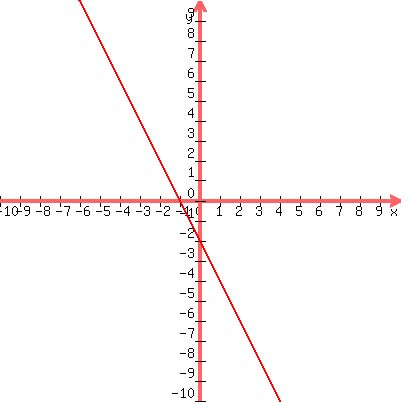
graph%28400%2C400%2C-10%2C10%2C-10%2C10%2C-2x-2%29


You'll notice that G(x) is simply F(x)'s function flipped along the x axis and moved down 2. It's as simple as that! Any questions, feel free to ask.