SOLUTION: FOR THE FUNCTION DEFINED BY {{{f(x)=2-x^2}}},{{{0<x}}}, USE A SKETCH TO HELP FIND A FORMULA FOR f^-1(x).

Algebra ->  Functions -> SOLUTION: FOR THE FUNCTION DEFINED BY {{{f(x)=2-x^2}}},{{{0<x}}}, USE A SKETCH TO HELP FIND A FORMULA FOR f^-1(x).      Log On


   

Question 64824: FOR THE FUNCTION DEFINED BY f%28x%29=2-x%5E2,0%3Cx, USE A SKETCH TO HELP FIND A FORMULA FOR f^-1(x).
Answer by funmath(2933) About Me  (Show Source):
You can put this solution on YOUR website!
FOR THE FUNCTION DEFINED BY f%28x%29=2-x%5E2,0%3Cx, USE A SKETCH TO HELP FIND A FORMULA FOR f^-1(x).
f%28x%29=2-x%5E2 Is graphed below. Ignore the left side of the graph because the domain includes only positive values. I have also graphed the line y=x, because inverse functions are reflected about that line.
graph%28300%2C200%2C-10%2C10%2C-10%2C10%2C2-x%5E2%2Cx%29
Notice that the graph has a y-intercept of (0,2), therefore the inverse will have an x-intercept of (2,0). Notice also that the graph goes toward -infinity as x goes towards +infinity, therefore its inverse will have x's that go to -infinity as y goes to positive infinity.
The parent f(x)=x^2, therefore the parent f^-1(x)=sqrt(x), it has a horizontal reflection so f^-1(x)=sqrt(-x). It also has a horizontal shift right 2 units, so the inverse function is:
f^-1(x)=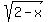sqrt%282-x%29
The graph of the inverse is below:
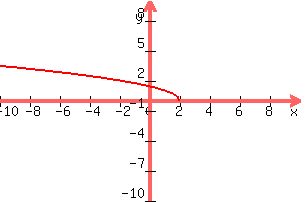
graph%28300%2C200%2C-10%2C10%2C-10%2C10%2Csqrt%282-x%29%29
If you aren't being taught about reflections and shifts, plot the points for f(x) and then reverse the x's and y's and you'll have the inverse.
Happy Calculating!!!