Question 647746: The points (4,2) and (-5,2) determine a unique line. Find the slope of this line.
Answer by Algebraic(50)  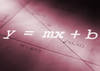 (Show Source): (Show Source):
You can put this solution on YOUR website! The slope of any line can be taken from the formula shown below:

M is the slope we will be trying to figure out, and the points (x^1 , y^1) and (x^2 , y^2) will be replaced with the ones given to you.
Look at the points given to you. The first coordinates are (4,2). This represents (x^1, y^1), and (-5,2) represents (x^2, y^2), so let's replace it into the equation.
Step 1:  Replace the coordinates given to you. Replace the coordinates given to you.
Step 2: 
Step 3: Solve within the parenthesis.. 
Step 4: The slope (M) is 0 (zero) because (0/9) is 0.
Answer: The slope of the line with the points (4,2) and (-5,2) is m = 0
|
|
|