Question 647522: A psychologist studied self-esteem scores and found the sample data set to be normally distributed with a mean of 50 and a standard deviation of 5.
Part A**What raw score cuts off the bottom 10.03% of this distribution?
Steps:
What is the z-score that cuts off the bottom 10.03% of this distribution?
What is the raw score that cuts off the bottom 10.03% of this distribution?
Part B**What percentage of the scores is between 57.5 and 65?
Steps:
What is the z-score that corresponds to the raw score of 57.5?
What is the z-score that corresponds to the raw score of 65?
What percentage of the scores is between 57.5 and 65?
Part C:**A raw score of 35 is associated with what percentile?
Steps:
What is the z-score associated with a raw score of 35?
A raw score of 35 is associated with what percentile?
Part D:**What raw scores mark the middle 34% of this distribution?
Steps:
What are the z-scores that mark the middle 34% of this distribution? The z-score below the mean is The z-score above the mean is
What is the raw score below the mean?
Found 2 solutions by swincher4391, stanbon:
Answer by swincher4391(1107)   (Show Source): (Show Source):
You can put this solution on YOUR website! A)
i)
By use of TI or table: invNorm(.1003,0,1) For P({{z
So, our z-score is -1.28.
ii)Z-score = (x-mean)/SD
-1.28 = (x-50)/5
-6.40 = x -50
44.50 = x
B) Use of TI:
P(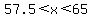 ) = normalcdf(57.5,65,50,5) = .0654 ) = normalcdf(57.5,65,50,5) = .0654
You cannot use a TI though, so convert 57.5 and 65 into z-scores Z1,Z2. Then with Z1 and Z2 take P(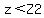 ) - P( ) - P(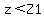 ) by use of table. ) by use of table.
Let's do that:
Z1 = (57.5-50)/5 = 7.5/5 = 1.5
Z2 = (65-50)/5 = 15/5 = 3
P(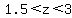 ) = P( ) = P( ) - P( ) - P(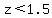 ) = .9986 - .9332 = .0654 ) = .9986 - .9332 = .0654
Or 6.54%
C) Z-score = (35-50)/5 = -15/5 = -3.
P(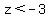 ) = 1-P( ) = 1-P( ) = 1- .9986 = .0014 ) = 1- .9986 = .0014
.14%
D)
34% of the data leaves the left tail to be (100-34)/2 = 33% and equally the right tail to be 33%
So to find the right most value, we need to find P(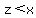 )=.67. )=.67.
By looking at at a table, you'll find that the z-score that achieves this is .44.
Next we need to find the left endpoint. P(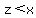 ) = .33. Similarly, by looking at a table we find that the z-score that achieves this is -.44 ) = .33. Similarly, by looking at a table we find that the z-score that achieves this is -.44
Convert z-scores to raw scores:
.44 = (x-50)/5
2.2 = x-50
x = 52.2
-.44 = (x-50)/5
-2.2 = x-50
x= 48.8
The one below the mean is 48.8.
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! A psychologist studied self-esteem scores and found the sample data set to be normally distributed with a mean of 50 and a standard deviation of 5.
Part A**What raw score cuts off the bottom 10.03% of this distribution?
Steps:
What is the z-score that cuts off the bottom 10.03% of this distribution?
z = invNorm(0.1003) = -1.280
What is the raw score that cuts off the bottom 10.03% of this distribution?
x = zs + u
x = -1.280*5 + 50 = 43.6
========================================
Part B**What percentage of the scores is between 57.5 and 65?
Steps:
What is the z-score that corresponds to the raw score of 57.5?
z(57.5) = (57.5-50)/5 = 1.5
---------------------------------
What is the z-score that corresponds to the raw score of 65?
z(65) = (65-50)/5 = 3
---
What percentage of the scores is between 57.5 and 65?
P(57.5<= x <=65) = P(1.5<= z <=3) = 0.0655 = 6.55%
------------------------------------------------------
Part C:**A raw score of 35 is associated with what percentile?
Steps:
What is the z-score associated with a raw score of 35?
z(35) = (35-50)/5 = -15/5 = -3
-------------------------------------
A raw score of 35 is associated with what percentile?
P(z < -3) = normalcdf(-100,-3) = 0.0013 = 0.13%
------------------------------------------------------
Part D:**What raw scores mark the middle 34% of this distribution?
Steps:
What are the z-scores that mark the middle 34% of this distribution?
The z-score below the mean is
z = invNorm(.50-0.17) = -0.44
----
The z-score above the mean is +0.44
---
What is the raw score below the mean?
x = -0.44*5+50 = 47.8
===========================
Cheers,
Stan H.
========================
|
|
|