Question 647381: Sam conducted a public opinion poll about the chances of candidates Rita and Paul winning the presidential election. Out of 1000 randomly chosen electors, 180 expressed their support for Rita. However candidate Rita believes that the proportion of electors who support her is 0.2.
Test at the 10% level whether candidate Rita is overestimating her support,
Thanking you in advance.
Answer by Sarpi(32)   (Show Source): (Show Source):
You can put this solution on YOUR website! We test H0: p = 0.20 vs Ha: p < 0.20 taking alpha = 10% (ie. the claim of candidate Rita)
Let: P^ be the proportion in the survey
Po be the proportion in the hypothesis
P^ = 180/1000 = 0.18 and Po = 0.20
Checking for 3 methods - confidence statements, critical boundaries and prob-value.
Method 1: Confidence statements
we test at the 90% cub for the proportion.
 Note the "P" after the < sign are P^ (ie P < P^ + Zalpha * sqrt(P^*(1-P^))/sqrt(n) Note the "P" after the < sign are P^ (ie P < P^ + Zalpha * sqrt(P^*(1-P^))/sqrt(n)
=> 
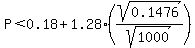


P < 0.1956
Since, Po = 0.20 is not inside the confidence upper bound (P < 0.1956), we reject the null hypothesis (H0)- Rita's claim.
Method 2: Critical Boundaries
We test for the critical lower bound





C = 0.1838
Since P^ = 0.18 is less than the critical lower bound (0.1838), we reject the null hypothesis (H0) - Rita's claim.
Method 3: The prob-value
We test the probability: P(P^<0.18)
=> 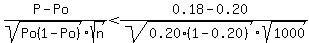

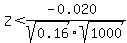
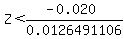
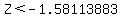
Then, normalcdf(-10,-1.58113883) with the help of "graphical calculator" or "normal distribution table"
normalcdf(-10,-1.58113883) = 0.0569
Since the prob-value, 0.0569 or 5.6% is less than alpha of 10%, we reject the null hypothesis (H0) - Rita's claim.
In all, we reject candidate Rita's claim that 20% of electorates support her.
Note: Either method applied, confidence or critical or prob-value, should give you the same conclusion - whether to reject or don't reject the H0.
|
|
|