Question 644062: please help me solve this Evaluate (if possible) the six trigonometric functions of the real number. (If not possible, enter IMPOSSIBLE.)
t = −π
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Trigonometric functions are defined based on a set of x-y coordinates and the unit circle.
The unit circle (with radius=1) is centered at point O(0,0), the origin.
Angles are considered as clockwise or counterclockwise turns from a starting side placed over the positive x-axis, as ray OA in the figure below.
The starting side is always in that standard position. The starting side of an angle is always the positive x-axis.
The sweep that is the angle ends on a ray called the terminal side.
Counterclockwise turns are considered positive angles; clockwise turns are considered negative angles.
Angles can be measured in degrees. In trigonometry, they are often measured in radians.
 If ray OA is turned counterclockwise until it coincides with ray OB, the angle swept can be measured as If ray OA is turned counterclockwise until it coincides with ray OB, the angle swept can be measured as 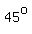 . .
The measure in radians is the distance traveled along the unit circle from point A to point B.
If ray OA is turned one whole turn counterclockwise, until it coincides with itself, the angle swept can be measured as  . In radians the measure would be . In radians the measure would be  , because the distance traveled along the circle is the whole circumference of the unit circle, whose length is , because the distance traveled along the circle is the whole circumference of the unit circle, whose length is 
Doing the whole turn clockwise would sweep an angle of 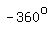 or, in radians or, in radians 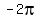 . .
An angle of  would correspond to half a turn counterclockwise from OA to OC, while an angle of would correspond to half a turn counterclockwise from OA to OC, while an angle of  would be half a turn clockwise from OA to OC. Both angles end in the same terminal side, and are called co-terminal. An infinite number of angle are co-terminal with those two. A would be half a turn clockwise from OA to OC. Both angles end in the same terminal side, and are called co-terminal. An infinite number of angle are co-terminal with those two. A  turn counterclockwise measures turn counterclockwise measures  is also co-terminal with is also co-terminal with  and and  , as would be a , as would be a  clockwise turn , which would measure clockwise turn , which would measure 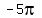 . .
The trigonometric functions are based on the coordinates of the point where the terminal side crosses the unit circle. For the angle AOC measuring  (and all the angles co-terminal with that angle) that point is C(-1,0). (and all the angles co-terminal with that angle) that point is C(-1,0).
The sine of the angle is the y-coordinate of that point, so  . .
The cosine of the angle is the x-coordinate of the point, so  . .
It is done the same way for any angle.
The other trigonometric functions (tangent, cotangent, secant and cosecant) can be calculated based on the sine and cosine of the same angle.




For  : :

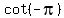 is undefined, because it would require dividing by is undefined, because it would require dividing by  . .
(I suppose they want you to write IMPOSSIBLE for an answer for 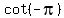 ). ).

 is also undefined, because it would require dividing by is also undefined, because it would require dividing by  . .
(I suppose they want you to write IMPOSSIBLE for that one too).
|
|
|