|
Question 643988: What is the sum of the first 900 consecutive odd numbers?
Found 3 solutions by Alan3354, MathLover1, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! What is the sum of the first 900 consecutive odd numbers?
-----------
that's the odd numbers 1 thru 1799
Add them in pairs.
1 + 1799 = 1800
3 + 1797 = 1800
etc
There are 450 pairs, each = 1800
Sum = 450*1800 = 810,000
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are two ways to do it. Here are both ways:
First way (without memorizing a frmula):
The 1st odd number is 1, 1 less than 2 which is twice 1.
The 2nd odd number is 3, 1 less than 4 which is twice 2.
The 3rd odd number is 5, 1 less than 6 which is twice 3.
So using that pattern
The 900th odd number is 1 less than twice 900, which is 1800, so the
900th odd number is 1799
Suppose the sum = N, then
N = 1 + 3 + 5 + 7 + ··· + 1793 + 1795 + 1797 + 1799
N also equals that same sum with the numbers added in the reverse order:
N = 1799 + 1797 + 1795 + 1793 + ··· + 7 + 5 + 3 + 1
Now let's write those two equations one under the other, and add equals
to equals term by term:
N = 1 + 3 + 5 + 7 + ··· + 1793 + 1795 + 1797 + 1799
N = 1799 + 1797 + 1795 + 1793 + ··· + 7 + 5 + 3 + 1
----------------------------------------------------------------
2N = 1800 + 1800 + 1800 + 1800 + ··· + 1800 + 1800 + 1800 + 1800
Since we know there are 900 terms on the right, that sum on the right is
900 times 1800 or 1620000, so that equation bercomes
2N = 1620000
Dividing both sides by 2
N = 810000
--------------------
The other way is to memorize the arithmetic series sum formula:
Sn =  [2·a1 + (n-1)·d]
Where n=900, a1=1 because it is the 1st odd integer, and d=2,
because consecutive odd numbers differ by 2.
S900 = [2·a1 + (n-1)·d]
Where n=900, a1=1 because it is the 1st odd integer, and d=2,
because consecutive odd numbers differ by 2.
S900 = 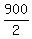 [2·(1) + (900-1)·(2)]
S900 = 450[2 + (899)·(2)]
S900 = 450[2 + 1798]
S900 = 450[1800]
S900 = 810000
Edwin [2·(1) + (900-1)·(2)]
S900 = 450[2 + (899)·(2)]
S900 = 450[2 + 1798]
S900 = 450[1800]
S900 = 810000
Edwin
|
|
|
| |