Question 643932: Can someone help me with this. Thanks for your time on this.
1. What is the largest integer power of two that is less than 665?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I know that  , and that helps me figure out that , and that helps me figure out that  is the larges power of 2 with an integer exponent that is less than 665. is the larges power of 2 with an integer exponent that is less than 665.
If/when I did not remember that,
I would calculate



and so on, so


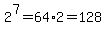
 and and

Of course I would not write all that just to calculate 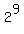 . I would just write the results one after the other or one above the other: . I would just write the results one after the other or one above the other:
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,
and then I would count to find that 512 is the 9th number in that geometric sequence/progression,
so it is thwe product of 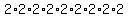 with nine twos, so it's with nine twos, so it's 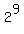 . .
|
|
|