Question 643275: I don't understand how to solve this question: At McDonald's, you can order McNuggets in boxes containing 6, 9, or 20 pieces. By ordering two boxes of 6, you can get 12 McNuggets. However you cannot order exactly 12, since no combination of 6, 9, and 20 adds up to 13. What is the greatest # of McNuggets that you CANNOT order? Include a clear explanation of how you solved the problem. Be prepared to defend your response.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is probably a much more streamlined, elegant solution, but I could not think of it yet.
Besides, I cannot speak the modular arithmetic language, and I do not know how what you are expected to know about it.
If you need the streamlined, elegant solution, ask the folks at the artofproblemsolving.com forum.
MY CLUMSY SOLUTION ( and and  represent positive integers): represent positive integers):
Combining only boxes of 6 and 9 nuggets, you can get only numbers of nuggets that are multiples of 3.
You cannot get 3 nuggets, but you can get amounts including all the multiples of 3 from 6 on.
For even multiples of 3, of the form 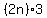 , ,
since  , ,
you can just use  boxes of 6. boxes of 6.
For odd multiples of 3, of the form 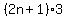 , ,
since  , ,
you can just use 1 box of 9 and 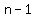 boxes of 6. boxes of 6.
Numbers that are not multiples of 3, require using at least 1 box of 20 nuggets.
Numbers that are not multiples of 3, are either 1 less than a multiple of 3, or 1 more than a multiple of 3. We can represent them as  and and 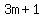 respectively. respectively.
The number 20 is of the form  , because , because  . .
Using 1 box of 20 nuggets, you can get 20 nuggets, 20+6=26, or 20+9=29, or 20 plus any other larger multiple of 3.
In other words, you cannot get 23, but you can get all the numbers of the form  starting from 26. starting from 26.
Numbers of the form 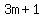 will require 2 boxes of 20 nuggets. will require 2 boxes of 20 nuggets.
Since  , with 2 boxes of 20 nuggets, you can get all the numbers of the form , with 2 boxes of 20 nuggets, you can get all the numbers of the form 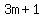 too, but only starting from too, but only starting from  . .
The previous number of the form 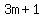 is 43, which cannot be formed by adding multiples of 20, 6, and 9. is 43, which cannot be formed by adding multiples of 20, 6, and 9.
The number  is the largest number that cannot be formed by adding multiples of 20, 6, and 9. is the largest number that cannot be formed by adding multiples of 20, 6, and 9.
|
|
|