SOLUTION: I need help with these problems can you solve these out for me in steps? Set 5 1. factor completely: x to the 2nd power -7x -30 2. factor completely: x to the 2nd power +

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: I need help with these problems can you solve these out for me in steps? Set 5 1. factor completely: x to the 2nd power -7x -30 2. factor completely: x to the 2nd power +       Log On


   

Question 6428: I need help with these problems can you solve these out for me in steps?
Set 5
1. factor completely: x to the 2nd power -7x -30
2. factor completely: x to the 2nd power + 4x -16
3. factor completely: 2x to the 2nd power -11x+5
4. factor completely: 4x to the 2nd power +20x-24
5. factor completely: 4m to the 2nd power - 9
6. factor completely: 16a to the 2nd power - 25b to the 2nd power
7. solve by factoring: x to the 2nd power -x-12=0
8. solve by factoring: 2c to the 2nd power -5=-9c
9. solve the equation:(x+6)(x-7)(x-8)(x+9)=0
10. find the dimensions of the rectangle if the width is 3 feet less than the length and the area is 40ft to the 2nd power
Answer by ichudov(507) About Me  (Show Source):
You can put this solution on YOUR website!
I'll do a couple for you....
Solved by pluggable solver: EXPLAIN simplification of an expression
Your Result:


YOUR ANSWER


  • This is an equation! Solutions: x=-6,x=7,x=8,x=-9.
  • Graphical form: Equation %28x%2B6%29%2A%28x-7%29%2A%28x-8%29%2A%28x%2B9%29=0 was fully solved.
  • Text form: (x+6)*(x-7)*(x-8)*(x+9)=0 simplifies to 0=0
  • Cartoon (animation) form: simplify_cartoon%28+%28x%2B6%29%2A%28x-7%29%2A%28x-8%29%2A%28x%2B9%29=0+%29
    For tutors: simplify_cartoon( (x+6)*(x-7)*(x-8)*(x+9)=0 )
  • If you have a website, here's a link to this solution.

DETAILED EXPLANATION

Look at highlight_red%28+%28x%2B6%29+%29%2A%28x-7%29%2A%28x-8%29%2A%28x%2B9%29=0.
Notes known roots (x-(-6))
Look at highlight_red%28+%28highlight_red%28+1+%29%29%2A%28x-7%29%2A%28x-8%29%2A%28x%2B9%29+%29=0.
Remove unneeded parentheses around factor highlight_red%28+1+%29
It becomes highlight_green%28+1+%29%2A%28x-7%29%2A%28x-8%29%2A%28x%2B9%29=0.
Look at highlight_red%28+1+%29%2A%28x-7%29%2A%28x-8%29%2A%28x%2B9%29=0.
Remove extraneous '1' from product highlight_red%28+1+%29
It becomes %28x-7%29%2A%28x-8%29%2A%28x%2B9%29=0.
Look at highlight_red%28+%28x-7%29+%29%2A%28x-8%29%2A%28x%2B9%29=0.
Notes known roots (x-(7))
Look at highlight_red%28+%28highlight_red%28+1+%29%29%2A%28x-8%29%2A%28x%2B9%29+%29=0.
Remove unneeded parentheses around factor highlight_red%28+1+%29
It becomes highlight_green%28+1+%29%2A%28x-8%29%2A%28x%2B9%29=0.
Look at highlight_red%28+1+%29%2A%28x-8%29%2A%28x%2B9%29=0.
Remove extraneous '1' from product highlight_red%28+1+%29
It becomes %28x-8%29%2A%28x%2B9%29=0.
Look at highlight_red%28+%28x-8%29+%29%2A%28x%2B9%29=0.
Notes known roots (x-(8))
Look at highlight_red%28+%28highlight_red%28+1+%29%29%2A%28x%2B9%29+%29=0.
Remove unneeded parentheses around factor highlight_red%28+1+%29
It becomes highlight_green%28+1+%29%2A%28x%2B9%29=0.
Look at highlight_red%28+1+%29%2A%28x%2B9%29=0.
Remove extraneous '1' from product highlight_red%28+1+%29
It becomes %28x%2B9%29=0.
Look at highlight_red%28+%28x%2B9%29+%29=0.
Remove unneeded parentheses around terms highlight_red%28+x+%29,highlight_red%28+9+%29
It becomes highlight_green%28+x+%29%2Bhighlight_green%28+9+%29=0.
Look at highlight_red%28+x%2B9+%29=0.
Solved linear equation highlight_red%28+x%2B9=0+%29 equivalent to x+9 =0
It becomes highlight_green%28+0+%29=0.
Result: 0=0
This is an equation! Solutions: x=-6,x=7,x=8,x=-9.

Universal Simplifier and Solver


Done!

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 2x%5E2%2B-11x%2B5+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-11%29%5E2-4%2A2%2A5=81.

Discriminant d=81 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--11%2B-sqrt%28+81+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-11%29%2Bsqrt%28+81+%29%29%2F2%5C2+=+5
x%5B2%5D+=+%28-%28-11%29-sqrt%28+81+%29%29%2F2%5C2+=+0.5

Quadratic expression 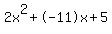2x%5E2%2B-11x%2B5 can be factored:
2x%5E2%2B-11x%2B5+=+2%28x-5%29%2A%28x-0.5%29
Again, the answer is: 5, 0.5. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+2%2Ax%5E2%2B-11%2Ax%2B5+%29