Question 642613: The height of a right-angled triangle is 1 m more than its base and its hypotenuse is 2 m more than its base. Find the height of the triangle?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  be the length of the base, in meters. be the length of the base, in meters.
Then,  is the height, in meters, and is the height, in meters, and
the length of the hypotenuse, in meters is 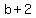 . .
Any of the sides of a triangle can be called the base,
but in this case, we know that it is not the hypotenuse,
because the problem says that the hypotenuse is 2 m longer than the base.
So the base is one of the leg of the right triangle.
The other leg, being perpendicular is the height.
Using the Pythagorean relationship between the lengths of the legs and the hypotenuse of a right triangle, we can write

Then we simplify the equation:
 --> -->  --> -->  --> --> 
Now, we solve the quadratic equation for  . .
The easiest way is factoring the quadratic polynomial on the left hand side:
 --> --> 
The solutions to the equation are the values of  that make one of those factors zero. that make one of those factors zero.
 ---> --->  is a solution of the equation, but a negative number cannot be the length of the base of a triangle. is a solution of the equation, but a negative number cannot be the length of the base of a triangle.
 ---> --->  is the only solution for the length of the base of the triangle. is the only solution for the length of the base of the triangle.
Then, the height, in meters is  . .
The triangle has side length in the ratio 3:4:5.
 and (3,4,5) is the most popular of the Pythagorean triples. and (3,4,5) is the most popular of the Pythagorean triples.
Teachers love it and it is the only one I remember.
|
|
|