|
Question 640968: three times the first of three consecutive odd integers is 3 more than twice the third. find the third integer?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the last/greatest of the three consecutive odd integers be  . .
(I like  . You could use . You could use  if you like that better). if you like that better).
We state that  has to be odd. has to be odd.
(If the  we find turns to be something that is not an odd integer, then the problem has no solution). we find turns to be something that is not an odd integer, then the problem has no solution).
The odd integer before  is is 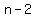 , and the odd integer before that is , and the odd integer before that is 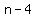 . .
The three consecutive odd integers, in order, are:
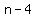 , , 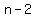 , and , and  . .
Three times the first is 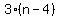 . .
Twice the third one is  , and 3 more than that is , and 3 more than that is 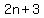 . .
Our equation is
 . .
To solve, we first apply the distributive property to do the multiplication on the left side of the equal sign.
 --> -->  --> --> 
Next, we subtract  from both sides of the equal sign: from both sides of the equal sign:
 --> -->  --> --> 
Then we add 12 to both sides of the equal sign:
 --> -->  --> --> 
The third of the three consecutive odd integers is  . .
The three consecutive odd integers are 11, 13, and 15, and 3 times the first,  , is 3 more than twice the third ( , is 3 more than twice the third ( and and  ). ).
|
|
|
| |